Question

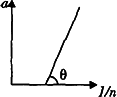
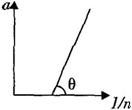
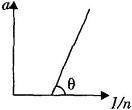
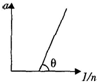n个相同木块排成一条直线用绷紧的细绳连在一起构成木块组静止置于水平面，当改变木块个数时，木块组先后在相同的水平力作用下做匀变速运动，木块组加速度a与木块个数的倒数

1

n

的关系如图所示，若更换木块组所在水平面的材料，再重复这个实验，则图线与水平轴的夹角θ将（　　）

A．变大

B．不变

C．变小

D．与水平面材料有关

Answer 1

分析：先对n个木块整体受力分析，受重力、支持力、拉力和滑动摩擦力，根据牛顿第二定律列式求解出加速度的表达式进行讨论即可．

解答：解：对n个木块整体受力分析，受重力、支持力、拉力和滑动摩擦力，根据牛顿第二定律，有：
F-μ（nmg）=（nm）a
解得：a=

F

nm

-μg=

F

m

?

1

n

-μg
故a-

1

n

图象的斜率等于

F

m

，等于tanθ，与n的大小无关，故n减小，θ不变；
故选B．

点评：本题关键是根据牛顿第二定律推导出加速度a的表达式并结合a-

1

n

图象分析，不难．