题目内容
如图所示，两块大小不同、质量分别为M和m的圆形薄板（厚度不计），半径分别为R和r，M=3m，两板之间用一根长为L=0.40 m的轻绳相连接.开始时，两板水平放置并叠合在一起处于静止状态，在其正下方0.80 m处有一固定支架C，支架上有一半径为R′(r＜R′＜R)的圆孔，圆孔与两薄板中心均在圆孔中心轴线上.今使两板一起自由下落，空气阻力不计，大板与支架C发生没有机械能损失的弹性碰撞，碰撞后两板即分离，直到轻绳绷紧，在轻绳绷紧的瞬间，两板便获得共同速度，g取10 m/s2.试求这个共同速度的大小.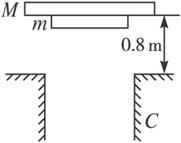
解析：开始两板做自由落体运动，设两板与支架C碰撞前的速度为v0，则：
v0=
m/s=4.0 m/s
M板与支架C碰撞没有机械能损失，故以v0反弹，做竖直上抛运动,而m板以v0做竖直下抛运动.以m板为参考系，设从两板分离到轻绳绷紧前的时间为t，则：L=2v0t
解得：t=
s=5.0×10-2s
从M板反弹起到轻绳拉直前瞬间，m的速度为v1，M的速度为v2
则v1=v0+gt=(4.0+10×0.05) m/s=4.5 m/s,方向竖直向下
v2=v0-gt=(4.0-10×0.05) m/s=3.5 m/s,方向竖直向上
在轻绳绷紧瞬间，系统动量近似守恒，选向下为正方向,则mv1-Mv2=(m+M)v
解得:v=
=-1.5 m/s，负号表示速度方向竖直向上.
答案：1.5 m/s
练习册系列答案
名校课堂系列答案
相关题目
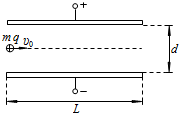如图所示，两块相同的金属板正对着水平放置，金属板长为L，两板间距离为d．上极板的电势比下极板高U．质量为m、带电量为q的正离子束，沿两板间中心轴线以初速度υ0进入两板间，最终都能从两板间射出．不计离子重力及离子间相互作用的影响．
（2012?浙江）如图所示，两块水平放置、相距为d的长金属板接在电压可调的电源上．两板之间的右侧区域存在方向垂直纸面向里的匀强磁场．将喷墨打印机的喷口靠近上板下表面，从喷口连续喷出质量均为m、水平速度均为v0、带相等电荷量的墨滴．调节电源电压至U，墨滴在电场区域恰能沿水平向右做匀速直线运动；进入电场、磁场共存区域后，最终垂直打在下板的M点．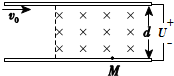
如图所示，两块水平放置、相距为d=0.5m的长金属板接在电压可调的电源上．两板之间的右侧区域存在方向垂直纸面向里的匀强磁场，磁感应强度为B=2T．将喷墨打印机的喷口靠近上板下表面，从喷口连续不断喷出质量均为m=3.2×10-3kg、速度水平且大小均为v0=5m/s、电荷量相等的墨滴．调节电压U至1V时，墨滴在电场区域恰能向右做匀速直线运动，并垂直磁场左边界进入电场、磁场共存区域后，最终打在下板的M点．
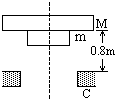如图所示，两块大小不同、质量分别为M和m的圆形薄板(厚度不计)，半径分别为R和r，M=3m，两板之间用一根长为L=0.4m的轻绳相连结，开始时两板水平放置并叠合在一起处在静止状态，在其正下方0.8m处有一固定支架C，支架上有一半径为R'(r＜R'＜R)的圆孔，圆孔与两薄板中心均在圆孔中心轴线上，今使两板一起无初速自由下落，空气阻力忽略不计．大板与支架C发生没有机械能损失的弹性碰撞，碰撞后，两块板即分离，直到轻绳绷紧，在轻绳绷紧的瞬间，两板便获得共同速度．试求这个共同速度的大小．(g取m/
)