题目内容
20. “嫦娥奔月”的过程可简化为:“嫦娥一号”升空后,绕地球沿椭圆轨道运动,远地点A距地面高度h1,然后经过变轨被月球捕获,再经过多次变轨,最终在距离月球表面h2的轨道上绕月球做匀速圆周运动(引力常量为G).
“嫦娥奔月”的过程可简化为:“嫦娥一号”升空后,绕地球沿椭圆轨道运动,远地点A距地面高度h1,然后经过变轨被月球捕获,再经过多次变轨,最终在距离月球表面h2的轨道上绕月球做匀速圆周运动(引力常量为G).(1)已知地球半径为R1,表面的重力加速度为g,求“嫦娥一号”在远地点A处的加速度a;
(2)已知“嫦娥一号”绕月运行的周期T,半径为R2,求月球的质量.
分析 (1)嫦娥一号受到合力为地球的万有引力,由牛顿第二定律可以求出A点处的加速度.
(2)月球对嫦娥一号的万有引力提供向心力,由牛顿第二定律可以求出月球的质量.
解答 解:(1)由牛顿第二定律得:
对嫦娥一号卫星:ma=G$\frac{Mm}{{r}^{2}}$=G$\frac{Mm}{({R}_{1}+{h}_{1})^{2}}$,
在地球表面的物体mg0=G$\frac{Mm}{{R}_{1}^{2}}$,
解得:a=$\frac{{R}_{1}^{2}{g}_{0}}{({R}_{1}+{h}_{1})^{2}}$;
(2)月球的万有引力提供向心力,由牛顿第二定律得:
G $\frac{Mm}{({R}_{2}^{\;}+{h}_{2})^{2}}$=m($\frac{2π}{T}$)2(R2+h2),
解得:M=$\frac{4{π}^{3}({R}_{2}+{h}_{2})^{3}}{G{T}^{2}}$
答:(1)“嫦娥一号”在远地点A处的加速度a为$\frac{{R}_{1}^{2}{g}_{0}}{{({R}_{1}+{h}_{1})}^{2}}$;
(2)月球的质量为$\frac{4{π}^{3}{({R}_{2}+{h}_{2})}^{3}}{G{T}^{2}}$.
点评 万有引力等于重力,万有引力提供向心力,由万有引力定律及牛顿第二定律可以正确解题.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
11.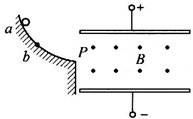 如图所示,带电平行板中存在有垂直纸面向外匀强磁场,某带电小球沿光滑绝缘轨道上的a点由静止开始下滑,经过轨道末端P点后进入平行板间恰好能沿水平方向作直线运动.现使小球从较低的b点开始下滑,经P点进入板间,则带电小球在平行板间的运动过程中下列说法正确的是( )
如图所示,带电平行板中存在有垂直纸面向外匀强磁场,某带电小球沿光滑绝缘轨道上的a点由静止开始下滑,经过轨道末端P点后进入平行板间恰好能沿水平方向作直线运动.现使小球从较低的b点开始下滑,经P点进入板间,则带电小球在平行板间的运动过程中下列说法正确的是( )
 如图所示,带电平行板中存在有垂直纸面向外匀强磁场,某带电小球沿光滑绝缘轨道上的a点由静止开始下滑,经过轨道末端P点后进入平行板间恰好能沿水平方向作直线运动.现使小球从较低的b点开始下滑,经P点进入板间,则带电小球在平行板间的运动过程中下列说法正确的是( )
如图所示,带电平行板中存在有垂直纸面向外匀强磁场,某带电小球沿光滑绝缘轨道上的a点由静止开始下滑,经过轨道末端P点后进入平行板间恰好能沿水平方向作直线运动.现使小球从较低的b点开始下滑,经P点进入板间,则带电小球在平行板间的运动过程中下列说法正确的是( )| A. | 小球带正电 | |
| B. | 小球将能再次沿水平方向作直线运动 | |
| C. | 小球所受的洛伦兹力将会减小 | |
| D. | 小球的电势能和动能都增大 |
8.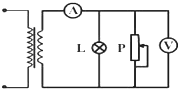 如图为一理想变压器,现在原线圈两端加上正弦式交变电压U=30$\sqrt{2}$sin(100πt)V,灯泡L的额定电压为6V且正常发光,电压表和电流表可视为理想电表.则下列说法中正确的是( )
如图为一理想变压器,现在原线圈两端加上正弦式交变电压U=30$\sqrt{2}$sin(100πt)V,灯泡L的额定电压为6V且正常发光,电压表和电流表可视为理想电表.则下列说法中正确的是( )
 如图为一理想变压器,现在原线圈两端加上正弦式交变电压U=30$\sqrt{2}$sin(100πt)V,灯泡L的额定电压为6V且正常发光,电压表和电流表可视为理想电表.则下列说法中正确的是( )
如图为一理想变压器,现在原线圈两端加上正弦式交变电压U=30$\sqrt{2}$sin(100πt)V,灯泡L的额定电压为6V且正常发光,电压表和电流表可视为理想电表.则下列说法中正确的是( )| A. | 原、副线圈的匝数之比为5$\sqrt{2}$:1 | |
| B. | 该交流电的频率为100Hz | |
| C. | 若将变阻器的滑片P向上滑动,电流表读数变大,电压表读数不变 | |
| D. | 若将变阻器的滑片P向上滑动,变压器的输出功率变小 |
5.如图所示,质量为m的物体,在力F的作用下,静止于竖直墙面上,则下列说法正确的是( )
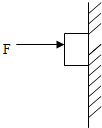

| A. | 物体受到竖直向上的静摩擦力的作用 | |
| B. | 物体受到竖直向上的滑动摩擦力的作用 | |
| C. | 物体所受摩擦力随F的增大而增大 | |
| D. | 物体所受摩擦力大小为mg |
12.一物体在光滑水平面上向右运动,从某时刻起对物体作用一恒定阻力使物体逐渐减速,直到停止,则物体在这段时间内通过的位移由下列哪个物理量完全决定( )
| A. | 物体的质量 | B. | 物体的初速度 | C. | 物体的初动能 | D. | 无法确定 |
9.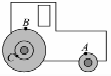 如图所示,某拖拉机后轮半径是前轮半径的2倍,A、B分别是前后轮轮缘上的点,C是后轮某半径的中点.拖拉机正常行驶时,A、B、C三点的线速度大小分别为vA、vB、vC,角速度大小分别为ωA、ωB、ωC,向心加速度大小分别为aA、aB、aC.以下选项正确的是( )
如图所示,某拖拉机后轮半径是前轮半径的2倍,A、B分别是前后轮轮缘上的点,C是后轮某半径的中点.拖拉机正常行驶时,A、B、C三点的线速度大小分别为vA、vB、vC,角速度大小分别为ωA、ωB、ωC,向心加速度大小分别为aA、aB、aC.以下选项正确的是( )
 如图所示,某拖拉机后轮半径是前轮半径的2倍,A、B分别是前后轮轮缘上的点,C是后轮某半径的中点.拖拉机正常行驶时,A、B、C三点的线速度大小分别为vA、vB、vC,角速度大小分别为ωA、ωB、ωC,向心加速度大小分别为aA、aB、aC.以下选项正确的是( )
如图所示,某拖拉机后轮半径是前轮半径的2倍,A、B分别是前后轮轮缘上的点,C是后轮某半径的中点.拖拉机正常行驶时,A、B、C三点的线速度大小分别为vA、vB、vC,角速度大小分别为ωA、ωB、ωC,向心加速度大小分别为aA、aB、aC.以下选项正确的是( )| A. | vA:vB:vC=2:2:1 | B. | ωA:ωB:ωC=2:1:2 | C. | aA:aB:aC=4:2:1 | D. | aA:aB:aC=1:2:1 |
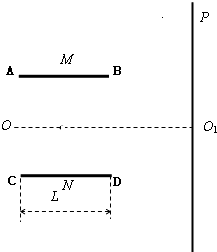 如图所示,M和N是相互平行的金属板,OO1为中线,P是足够大的荧光屏.金属板M和N相距为d,板长为L1.平行极板右端到荧光屏的距离为L2.
如图所示,M和N是相互平行的金属板,OO1为中线,P是足够大的荧光屏.金属板M和N相距为d,板长为L1.平行极板右端到荧光屏的距离为L2.