题目内容
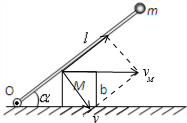
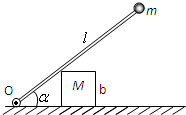如图所示，在水平面上放一边长为b的立方体木块M，木块上搁有一根长为l的轻质杆，杆端固定质量为m的均质小球（可视为质点），另一端铰接于O．不计摩擦阻力，由静止释放木块，当杆与水平面间夹角为α时小球获得最大速度，大小为vm．此时杆对木块作用力的大小为________，木块向右的速度为________．
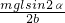
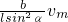
分析：杆与水平面间夹角为α时小球获得最大速度，说明此时杆处于平衡态，根据力矩平衡条件列式求解支持力；
将滑块上与杆接触的点的速度沿着平行杆和垂直杆正交分解，垂直杆分量等于杆上与滑块接触的点的速度．
解答：杆与水平面间夹角为α时小球获得最大速度，说明此时杆处于平衡态，根据力矩平衡条件，有：
N
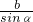=mgl?cosα解得：N=
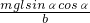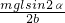=；杆上与滑块接触的点的速度为：v=ω?r=
；将滑块上与杆接触的点的速度沿着平行杆和垂直杆正交分解，如图
故滑块的速度为：vM=
=
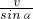；故答案为：
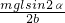，．点评：本题关键找准合运动和分运动，同时要能结合正交分解法和力矩平衡条件列式求解．
练习册系列答案
优学名师名题系列答案
相关题目
如图所示，在水平面上向右运动的物体，质量为4kg，物体与水平面的动摩擦因数μ=0.5，在运动过程中，还受到一个水平向左的大小为10N的拉力的作用，则物体受到的滑动摩擦力为（g取10m/s2）（ ）
如图所示，在水平面上有三个质量分别为m1，m2，m3的木块，木块1和2、2和3间分别用一原长为L、劲度系数为K的轻弹簧连接起来，木块1、2与水平面间的动摩擦因数为μ，木块3和水平面之间无摩擦力．现用一水平恒力向右拉木块3，当木块一起匀速运动时，1和3两木块间的距离为（木块大小不计）（ ）
如图所示，在水平面上固定三个完全相同的木块，一颗子弹以水平速度v射入，若子弹在木块中做匀减速直线运动，当穿透第三块木块时速度恰好为零，则子弹依次射入每个木块时的速度之比和穿过每个木块所用时间之比分别为（ ）
（2012?长宁区一模）如图所示，在水平面上放一边长为b的立方体木块M，木块上搁有一根长为l的轻质杆，杆端固定质量为m的均质小球（可视为质点），另一端铰接于O．不计摩擦阻力，由静止释放木块，当杆与水平面间夹角为α时小球获得最大速度，大小为vm．此时杆对木块作用力的大小为
如图所示，在水平面上有一固定的u形光滑金属框架，框架上放置一金属杆ab．在垂直纸面方向有一匀强磁场，下列情况中可能的是（ ）