题目内容
16. 如图所示,一个不计厚度上表面光滑的电动平板长L=3.75m,平板上左侧有一挡板,紧靠挡板处有一可看成质点的小球.开始时,平板与小球一起在水平面上向右做匀速运动,速度大小为v0=5m/s.某时刻平板开始制动,加速度大小a1=4m/s2.经过一段时间,小球从平板右端滑出并滑落到地面上接着在地面上做匀减速直线运动,运动t2=2.5s停下.求:
如图所示,一个不计厚度上表面光滑的电动平板长L=3.75m,平板上左侧有一挡板,紧靠挡板处有一可看成质点的小球.开始时,平板与小球一起在水平面上向右做匀速运动,速度大小为v0=5m/s.某时刻平板开始制动,加速度大小a1=4m/s2.经过一段时间,小球从平板右端滑出并滑落到地面上接着在地面上做匀减速直线运动,运动t2=2.5s停下.求:(1)小球在地面上做匀减速直线运动的加速度a2大小
(2)从开始制动到小球离开平板所用的时间t1
(3)最终小球离平板右端的距离s.
分析 (1)根据匀变速直线运动的速度时间公式求出小球在地面上匀减速直线运动的加速度大小.
(2)根据速度时间公式求出平板速度减为零的时间,求出此时平板和小球的位移,判断出小球还未离开平板,再结合位移公式求出小球继续运动的时间,从而得出从开始制动到小球离开平板所用的时间.
(3)小球离开平板后,平板已经停止,结合平均速度推论求出小球匀减速运动的位移,从而得出最终小球离平板右端的距离.
解答 解:(1)小球离开平板后做匀减速运动,根据速度时间关系,加速度为:
a2=$\frac{{v}_{0}}{{t}_{2}}$
代入数据解得:a2=2m/s2
(2)根据速度时间关系知,平板停止运动的时间为:
t=$\frac{{v}_{0}}{{a}_{1}}=\frac{5}{4}s=1.25s$.
在此过程中平板的位移:${x}_{平}=\frac{{v}_{0}}{2}t=\frac{5}{2}×1.25m=3.125m$,
此过程中小球的位移:x球=v0t=5×1.25m=6.25m
因为△x=x球-x平=6.25-3.125m=3.125m<L
所以小球还需运动的时间为:$△t=\frac{L-△x}{{v}_{0}}=\frac{3.75-3.125}{5}s=0.125s$,
所以小球离开平板的时间为:t总=t+△t=1.25+0.125s=1.375s
(3)小球离开平板时已经停止运动,故小球距平板右端的距离为小球在水平面上匀减速运动的位移,根据平均速度位移关系有:
s=$\frac{0+{v}_{0}}{2}{t}_{2}=\frac{0+5}{2}×2.5m=6.25m$.
答:(1)小球在地面上做匀减速直线运动的加速度a2大小为2m/s2;
(2)从开始制动到小球离开平板所用的时间为1.375s;
(3)最终小球离平板右端的距离为6.25m.
点评 掌握匀变速直线运动的速度时间关系、位移时间关系是正确解决问题的基础,不难,关键是注意判断平板匀减速运动时小球仍在匀速运动.

| A. | 上升和下落过程的位移一定相等 | |
| B. | 上升和下落过程的时间一定相等 | |
| C. | 上升和下落的平均速度大小一定相等 | |
| D. | 上升和下落过程中加速度不相同 |
| A. | $\frac{F}{Q}$ | B. | $\frac{F}{q}$ | C. | $\frac{kq}{{r}^{2}}$ | D. | $\frac{kQ}{{r}^{2}}$ |
 如图所示,是等量异种点电荷形成的电场,O是两电荷连线的中点(图中未画出).以O为圆心,以r为半径在垂直纸面内做圆(圆面与两电荷连线垂直),则下列关于圆周上的各点电场强度的说法,正确的是( )
如图所示,是等量异种点电荷形成的电场,O是两电荷连线的中点(图中未画出).以O为圆心,以r为半径在垂直纸面内做圆(圆面与两电荷连线垂直),则下列关于圆周上的各点电场强度的说法,正确的是( )| A. | 大小相等,方向不同 | B. | 大小相等,方向相同 | ||
| C. | 大小不相等,方向也不同 | D. | 大小不相等,但方向相同 |
| A. | 只有体积很小的物体才能看做质点 | |
| B. | 物体的加速度越来越大,速度变化一定越来越快 | |
| C. | 物体做直线运动时路程和位移大小相等 | |
| D. | 高速公路上的限速标识,限制的是平均速度 |
 如图所示,不计质量的光滑小滑轮用细绳悬挂于墙上O点,跨过滑轮的细绳连接物块A、B,物块A、B都处于静止状态.现将物块B向右移至C点后,物块A、B仍保持静止,下列说法中正确的是( )
如图所示,不计质量的光滑小滑轮用细绳悬挂于墙上O点,跨过滑轮的细绳连接物块A、B,物块A、B都处于静止状态.现将物块B向右移至C点后,物块A、B仍保持静止,下列说法中正确的是( )| A. | B与水平面间的摩擦力增大 | B. | 地面对B的支持力减小 | ||
| C. | 悬于墙上的绳所受拉力不变 | D. | A、B静止时,始终有α=β=θ成立 |
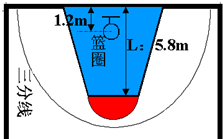 在一节篮球课中,某同学站在罚球线中央进行罚球表演(如图),关于篮球的位移和路程的说法正确的是( )
在一节篮球课中,某同学站在罚球线中央进行罚球表演(如图),关于篮球的位移和路程的说法正确的是( )| A. | 篮球的位移为4.6m | |
| B. | 罚球点到篮圈的直线距离为篮球的路程 | |
| C. | 篮球的飞行路线的长度是篮球的位移 | |
| D. | 篮球的路程总比篮球的位移长 |
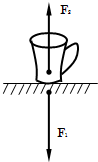
| A. | 力F1就是杯子的重力 | B. | 力F1和力F2是一对平衡力 | ||
| C. | 力F1是由杯子发生形变产生的 | D. | 力F1的大小大于力F2的大小 |