题目内容
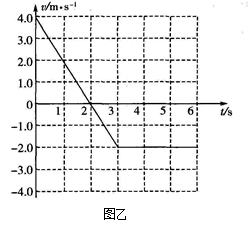
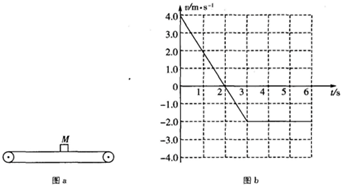
一足够长的水平传送带以恒定的速度运动,现将质量为M=2.0kg 的小物块抛上传送带,如图a所示.地面观察者记录了小物块抛上传送带后0~6s内的速度随时间变化的关系,如图b所示(取向右运动的方向为正方向),g 取10m/s2.

(1)指出传送带速度的大小和方向;
(2)计算物块与传送带间的动摩擦因数μ
(3)计算0-6s内传送带对小物块做的功.
(4)计算0-6s内由于物块与传送带摩擦产生的热量.
解:(1)由图可知速度大小为2m/s,方向向左.
(2)由速度图象可得,物块在滑动摩擦力作用下做匀变速运动的加速度为a,有a= .
.
由牛顿第二定律得,滑动摩擦力-f=Ma
其中f=μFN=μMg.
得到物块与传送带间的动摩擦因数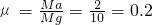 .
.
(3)传送带对小物块做的功,即为传送带对小物块的作用力对小物块做的功,由于重力和支持力不做功,故等于合外力对小物块做的功,根据动能定理有:
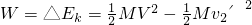
解得W=-12J.
(4)以传送带为参考系,物块以相对于传送带的速度v′=v2′+V=4+2=6m/s.
冲上传送带到相对静止的过程中,物块相对传送带通过位移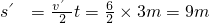 .
.
产生的热量Q=fs′=4×9=36J.
答:(1)传送带速度的大小为2m/s,方向向左.
(2)物块与传送带间的动摩擦因数μ为0.2.
(3)0-6s内传送带对小物块做的功-12J.
(4)0-6s内由于物块与传送带摩擦产生的热量为36J.
分析:物块滑上传送带后先做匀减速直线运动,然后反向做匀加速直线运动,当速度达到传送带速度做匀速直线运动,可知传送带的速度大小和方向.根据牛顿第二定律,结合小物块的加速度求出物块与传送带间的动摩擦因数.根据动能定理求出传送带对小物块做的功.求出物块与传送带的相对位移,通过功能关系Q=fs求出摩擦产生的热量,s为相对路程.
点评:解决本题的关键理清物块的运动规律,结合牛顿第二定律和运动学公式求解,对于第4问,也可以以地面为参考系,分别求出传送带和物块的位移,从而求出相对路程.
(2)由速度图象可得,物块在滑动摩擦力作用下做匀变速运动的加速度为a,有a=
 .
.由牛顿第二定律得,滑动摩擦力-f=Ma
其中f=μFN=μMg.
得到物块与传送带间的动摩擦因数
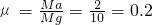 .
.(3)传送带对小物块做的功,即为传送带对小物块的作用力对小物块做的功,由于重力和支持力不做功,故等于合外力对小物块做的功,根据动能定理有:
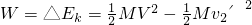
解得W=-12J.
(4)以传送带为参考系,物块以相对于传送带的速度v′=v2′+V=4+2=6m/s.
冲上传送带到相对静止的过程中,物块相对传送带通过位移
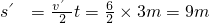 .
.产生的热量Q=fs′=4×9=36J.
答:(1)传送带速度的大小为2m/s,方向向左.
(2)物块与传送带间的动摩擦因数μ为0.2.
(3)0-6s内传送带对小物块做的功-12J.
(4)0-6s内由于物块与传送带摩擦产生的热量为36J.
分析:物块滑上传送带后先做匀减速直线运动,然后反向做匀加速直线运动,当速度达到传送带速度做匀速直线运动,可知传送带的速度大小和方向.根据牛顿第二定律,结合小物块的加速度求出物块与传送带间的动摩擦因数.根据动能定理求出传送带对小物块做的功.求出物块与传送带的相对位移,通过功能关系Q=fs求出摩擦产生的热量,s为相对路程.
点评:解决本题的关键理清物块的运动规律,结合牛顿第二定律和运动学公式求解,对于第4问,也可以以地面为参考系,分别求出传送带和物块的位移,从而求出相对路程.

练习册系列答案
相关题目
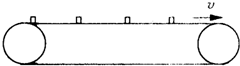 如图所示,一足够长的水平传送带以恒定的速度v运动,每隔时间T轻轻放上相同的物块,当物块与传送带相对静止后,相邻两物块的间距大小( )
如图所示,一足够长的水平传送带以恒定的速度v运动,每隔时间T轻轻放上相同的物块,当物块与传送带相对静止后,相邻两物块的间距大小( )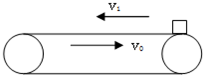 如图所示,有一足够长的水平传送带以v0=4m/s的速度匀速运动,现将一质量m=2kg的物体以水平向左的初速度v1=8m/s从右端滑上传送带,向左运动速度v2=0时距离传送带的右端x=8m,求
如图所示,有一足够长的水平传送带以v0=4m/s的速度匀速运动,现将一质量m=2kg的物体以水平向左的初速度v1=8m/s从右端滑上传送带,向左运动速度v2=0时距离传送带的右端x=8m,求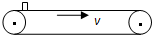 一足够长的水平传送带以恒定速率v运动,将一质量为m的物体轻放到传送带左端,设物体与传送带之间的摩擦因数为μ,则下列说法正确的是( )
一足够长的水平传送带以恒定速率v运动,将一质量为m的物体轻放到传送带左端,设物体与传送带之间的摩擦因数为μ,则下列说法正确的是( ) 内的速度随时间变化的关系,以水平向右的方向为正方向,得到小物块的v-t 图像如图乙所示。取
内的速度随时间变化的关系,以水平向右的方向为正方向,得到小物块的v-t 图像如图乙所示。取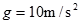 。
。