题目内容
9.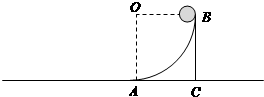 如图,质量为M的滑块ABC静置于光滑水平地面上,光滑弧面AB为圆弧,半径为R,O为其圆心,A在O点正下方.将质量为m的小球(可看成质点)从B点由静止释放.当小球运动到滑块最低点A点时,求:
如图,质量为M的滑块ABC静置于光滑水平地面上,光滑弧面AB为圆弧,半径为R,O为其圆心,A在O点正下方.将质量为m的小球(可看成质点)从B点由静止释放.当小球运动到滑块最低点A点时,求:(1)滑块运动的位移为多大?
(2)滑块运动的速度为多大?
分析 (1)滑块与小球组成的系统在水平方向动量守恒,应用动量守恒定律可以求出滑块的位移.
(2)滑块与小球在水平方向系统动量守恒,系统机械能守恒,应用动量守恒定律与机械能守恒定律可以求出滑块的速度.
解答 解:(1)滑块与小球组成的系统在水平方向动量守恒,以向左为正方向,
由动量守恒定律得:mv1-Mv2=0,即:m$\frac{R-x}{t}$-M$\frac{x}{t}$=0,解得:x=$\frac{mR}{M+m}$;
(2)滑块与小球组成的系统在水平方向动量守恒,
以向左为正方向,由动量守恒定律得:mv1-Mv2=0,
系统机械能守恒,由机械能守恒定律得:
mgR=$\frac{1}{2}$mv12+$\frac{1}{2}$Mv22,解得:v2=$\sqrt{\frac{2{m}^{2}gR}{M(M+m)}}$,方向:水平向右;
答:(1)滑块运动的位移为$\frac{mR}{M+m}$;
(2)滑块运动的速度为$\sqrt{\frac{2{m}^{2}gR}{M(M+m)}}$,方向:水平向右.
点评 本题考查了动量守恒定律的应用,分析清楚物体的运动过程是正确解题的关键,应用动量守恒定律与机械能守恒定律可以解题.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
19. 如图甲所示,小物体从竖直弹簧上方离地高h1处由静止释放,其动能Ek与离地高度h的关系如图乙所示,其中高度从h1下降到h2,图象为直线,其余部分为曲线,h3对应图象的最高点,轻弹簧劲度系数为k,小物体质量为m,重力加速度为g.以下说法正确的是( )
如图甲所示,小物体从竖直弹簧上方离地高h1处由静止释放,其动能Ek与离地高度h的关系如图乙所示,其中高度从h1下降到h2,图象为直线,其余部分为曲线,h3对应图象的最高点,轻弹簧劲度系数为k,小物体质量为m,重力加速度为g.以下说法正确的是( )
 如图甲所示,小物体从竖直弹簧上方离地高h1处由静止释放,其动能Ek与离地高度h的关系如图乙所示,其中高度从h1下降到h2,图象为直线,其余部分为曲线,h3对应图象的最高点,轻弹簧劲度系数为k,小物体质量为m,重力加速度为g.以下说法正确的是( )
如图甲所示,小物体从竖直弹簧上方离地高h1处由静止释放,其动能Ek与离地高度h的关系如图乙所示,其中高度从h1下降到h2,图象为直线,其余部分为曲线,h3对应图象的最高点,轻弹簧劲度系数为k,小物体质量为m,重力加速度为g.以下说法正确的是( )| A. | 小物体下降的整个过程中机械能守恒 | |
| B. | 小物体下落至高度h3时,加速度为0 | |
| C. | 弹簧弹性势能的最大值为mg(h1-h3) | |
| D. | 小物体从高度h2下降h4,弹簧弹性势能增加了$\frac{{{m}^{2}g}^{2}}{k}$ |
17. 如图所示,一条不可伸长的轻绳绕过光滑的轻质定滑轮分别与物块A、B相连,细绳两部分分别处于水平和竖直状态,桌面光滑,物块A和B的质量分别为M和m,重力加速度为g.现将系统由静止释放,在B落地前,下列判断正确的是( )
如图所示,一条不可伸长的轻绳绕过光滑的轻质定滑轮分别与物块A、B相连,细绳两部分分别处于水平和竖直状态,桌面光滑,物块A和B的质量分别为M和m,重力加速度为g.现将系统由静止释放,在B落地前,下列判断正确的是( )
 如图所示,一条不可伸长的轻绳绕过光滑的轻质定滑轮分别与物块A、B相连,细绳两部分分别处于水平和竖直状态,桌面光滑,物块A和B的质量分别为M和m,重力加速度为g.现将系统由静止释放,在B落地前,下列判断正确的是( )
如图所示,一条不可伸长的轻绳绕过光滑的轻质定滑轮分别与物块A、B相连,细绳两部分分别处于水平和竖直状态,桌面光滑,物块A和B的质量分别为M和m,重力加速度为g.现将系统由静止释放,在B落地前,下列判断正确的是( )| A. | 物体B下降的加速度大小为$\frac{mg}{M}$ | |
| B. | 物体B下降的加速度大小为$\frac{mg}{M+m}$ | |
| C. | 物体A对桌面的压力的大小等于桌面对A的支持的大小 | |
| D. | 轻绳的张力为mg |
4. 如图所示为磁流体发电机的原理图:将一束等离子体喷射入磁场,在场中有两块金属板A、B,这时金属板上就会聚集电荷,产生电压,如果射入的等离子体速度均为v,两金属板的板长为L,板间距离为d,板平面的面积为S,匀强磁场的磁感应强度为B,方向垂直于速度方向,负载电阻为R,电离气体充满两板间的空间.当发电机稳定发电时,电流表示数为I,下列说法正确的是( )
如图所示为磁流体发电机的原理图:将一束等离子体喷射入磁场,在场中有两块金属板A、B,这时金属板上就会聚集电荷,产生电压,如果射入的等离子体速度均为v,两金属板的板长为L,板间距离为d,板平面的面积为S,匀强磁场的磁感应强度为B,方向垂直于速度方向,负载电阻为R,电离气体充满两板间的空间.当发电机稳定发电时,电流表示数为I,下列说法正确的是( )
 如图所示为磁流体发电机的原理图:将一束等离子体喷射入磁场,在场中有两块金属板A、B,这时金属板上就会聚集电荷,产生电压,如果射入的等离子体速度均为v,两金属板的板长为L,板间距离为d,板平面的面积为S,匀强磁场的磁感应强度为B,方向垂直于速度方向,负载电阻为R,电离气体充满两板间的空间.当发电机稳定发电时,电流表示数为I,下列说法正确的是( )
如图所示为磁流体发电机的原理图:将一束等离子体喷射入磁场,在场中有两块金属板A、B,这时金属板上就会聚集电荷,产生电压,如果射入的等离子体速度均为v,两金属板的板长为L,板间距离为d,板平面的面积为S,匀强磁场的磁感应强度为B,方向垂直于速度方向,负载电阻为R,电离气体充满两板间的空间.当发电机稳定发电时,电流表示数为I,下列说法正确的是( )| A. | A板为磁流体发电机的正极 | B. | 外电路电流方向为B-R-A | ||
| C. | 板间电离气体的电阻率$\frac{S}{d}$($\frac{Bdv}{I}$-R) | D. | 板间电离气体的电阻率$\frac{S}{L}$($\frac{Bdv}{I}$-R) |
14. 将小球以10m/s的初速度从地面竖直向上抛出,取地面为零势能面,小球在上升过程中的动能Ek、重力势能Ep与上升高度h间的关系分别如图中两直线所示,设阻力大小恒定,取g=10m/s2,下列说法正确的是( )
将小球以10m/s的初速度从地面竖直向上抛出,取地面为零势能面,小球在上升过程中的动能Ek、重力势能Ep与上升高度h间的关系分别如图中两直线所示,设阻力大小恒定,取g=10m/s2,下列说法正确的是( )
 将小球以10m/s的初速度从地面竖直向上抛出,取地面为零势能面,小球在上升过程中的动能Ek、重力势能Ep与上升高度h间的关系分别如图中两直线所示,设阻力大小恒定,取g=10m/s2,下列说法正确的是( )
将小球以10m/s的初速度从地面竖直向上抛出,取地面为零势能面,小球在上升过程中的动能Ek、重力势能Ep与上升高度h间的关系分别如图中两直线所示,设阻力大小恒定,取g=10m/s2,下列说法正确的是( )| A. | 小球的重力为2N | |
| B. | 小球受到的阻力大小为0.25N | |
| C. | 小球动能与重力势能相等时的高度为$\frac{21}{9}$m | |
| D. | 小球上升到2m时,动能与重力势能之差为0.5J |
1.下列关于摩擦力的方向的说法,正确的是( )
| A. | 摩擦力的方向总是与物体运动的方向相反 | |
| B. | 滑动摩擦力的方向总是与物体运动的方向相反 | |
| C. | 摩擦力的方向不可能与物体运动的方向垂直 | |
| D. | 摩擦力的方向可能与物体运动的方向相同 |
 某同学为了测定一只电阻的阻值,采用了如下方法,用多用电表粗测,多用电表电阻挡有4个倍率:分别为×1K、×100、×10、×1,该同学选择×100倍率,用正确的操作步骤测量时,发现指针偏转角度太大(指针位置如图1中虚线所示),为了较准确地进行测量,请你补充完整下列依次应该进行的主要操作步骤:
某同学为了测定一只电阻的阻值,采用了如下方法,用多用电表粗测,多用电表电阻挡有4个倍率:分别为×1K、×100、×10、×1,该同学选择×100倍率,用正确的操作步骤测量时,发现指针偏转角度太大(指针位置如图1中虚线所示),为了较准确地进行测量,请你补充完整下列依次应该进行的主要操作步骤: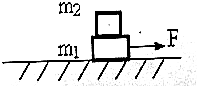 如图所示,质量为2kg的m1和质量为1kg的m2两个物体叠放在一起,放在水平面,m1与m2、m1与水平面间的动摩擦因数都是0.3,现用水平拉力F拉m1,使m1和m2一起沿水平面运动,要使m1和m2之间没有相对滑动,水平拉力F最大为多大?
如图所示,质量为2kg的m1和质量为1kg的m2两个物体叠放在一起,放在水平面,m1与m2、m1与水平面间的动摩擦因数都是0.3,现用水平拉力F拉m1,使m1和m2一起沿水平面运动,要使m1和m2之间没有相对滑动,水平拉力F最大为多大?