题目内容
13.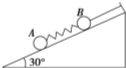 如图所示,A、B两小球分别连在弹簧两端,B端用细线固定在倾角为30°光滑斜面上,若不计弹簧质量,在线被剪断瞬间,A、B两球的加速度分别为( )
如图所示,A、B两小球分别连在弹簧两端,B端用细线固定在倾角为30°光滑斜面上,若不计弹簧质量,在线被剪断瞬间,A、B两球的加速度分别为( )| A. | 都等于$\frac{g}{2}$ | B. | $\frac{g}{2}$和0 | ||
| C. | $\frac{{M}_{A}+{M}_{B}}{{M}_{B}}$•$\frac{g}{2}$和0 | D. | 0和$\frac{{M}_{A}+{M}_{B}}{{M}_{B}}$•$\frac{g}{2}$ |
分析 悬线剪断前,以两球为研究对象,求出悬线的拉力和弹簧的弹力.突然剪断悬线瞬间,弹簧的弹力没有来得及变化,分析瞬间两球的受力情况,由牛顿第二定律求解加速度.
解答 解:线被剪断瞬间,线的拉力变为0,弹簧形变来不及发生变化,弹力不变,故A球仍受力平衡,加速度为0,B球受重力、支持力、弹簧产生的大小为MAg•sin 30°的弹力,所以可得其加速度为$\frac{(MA+MB)•g}{2MB}$.
答:D
点评 本题是动力学中典型的问题:瞬时问题,往往先分析悬线剪断前弹簧的弹力,再分析悬线判断瞬间物体的受力情况,再求解加速度,抓住悬线剪断瞬间弹力没有来得及变化.

练习册系列答案
相关题目
3.雅安大地震,牵动了全国人民的心.一架装载救灾物资的直升飞机,以10m/s的速度水平飞行,在距地面180m的高度处,欲将救灾物资准确投放至地面目标,若不计空气阻力,g取10m/s2,则( )
| A. | 物资投出后经过6s到达地面目标 | |
| B. | 物资投出后经过18s到达地面目标 | |
| C. | 应在距地面目标水平距离60m处投出物资 | |
| D. | 应在距地面目标水平距离180m处投出物资 |
4.关于合运动和分运动,下列说法不正确的是( )
| A. | 合运动和分运动的时间相同 | |
| B. | 由合运动分解为两个分运动,可以有两个不同的分解方法 | |
| C. | 物体做曲线运动时,才能将这个运动分解为两个分运动 | |
| D. | 任何形式的运动,都可以用几个分运动代替 |
1.对于万有引力定律的数学表达式F=G$\frac{Mm}{{r}^{2}}$,下列说法正确的是( )
| A. | 公式中G为引力常量,是有单位的,是人为规定的 | |
| B. | r趋近于零时,万有引力趋于无穷大 | |
| C. | 万有引力定律是牛顿发现的,G是卡文迪许利用扭秤测出来的 | |
| D. | M、m之间的万有引力总是大小相等方向相反,是一对平衡力 |
8.原子的质量主要集中在( )
| A. | 质子上 | B. | 中子上 | C. | 电子上 | D. | 原子核上 |
18.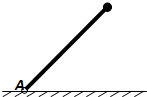 轻杆的一端通过光滑的绞链固定在地面上的A点,另一端固定一个质量为m的小球,最初杆处于水平地面上.当杆在外力的作用下由水平位置缓慢转到竖直位置的过程中,下列关于小球说法正确的是( )
轻杆的一端通过光滑的绞链固定在地面上的A点,另一端固定一个质量为m的小球,最初杆处于水平地面上.当杆在外力的作用下由水平位置缓慢转到竖直位置的过程中,下列关于小球说法正确的是( )
 轻杆的一端通过光滑的绞链固定在地面上的A点,另一端固定一个质量为m的小球,最初杆处于水平地面上.当杆在外力的作用下由水平位置缓慢转到竖直位置的过程中,下列关于小球说法正确的是( )
轻杆的一端通过光滑的绞链固定在地面上的A点,另一端固定一个质量为m的小球,最初杆处于水平地面上.当杆在外力的作用下由水平位置缓慢转到竖直位置的过程中,下列关于小球说法正确的是( )| A. | 所受弹力的方向一定沿杆 | B. | 所受弹力一直减小 | ||
| C. | 所受合力不变 | D. | 所受弹力始终做正功 |
5.有关光的本性,下列说法正确的是( )
| A. | 光具有波动性,又具有粒子性,这是互相矛盾和对立的 | |
| B. | 光的波动性类似于机械波,光的粒子性类似于质点 | |
| C. | 大量光子才具有波动性,个别光子具有粒子性 | |
| D. | 由于光具有波动性,又具有粒子性,无法只用其中一种去说明光的一切行为,光具有波粒二象性 |
2.从“神舟六号”载人飞船的发射成功可以预见,随着航天员在轨道舱内停留时间的增加,体育锻炼成了一个必不可少的环节,下列器材适宜航天员在轨道舱中进行锻炼的是( )
| A. | 哑铃 | B. | 弹簧拉力器 | C. | 单杠 | D. | 跑步机 |
1.图甲为一列简谐横波在某一时刻的波形图,图乙为质点P以此时刻为计时起点的振动图象.从该时刻起( )
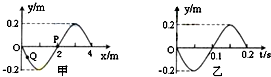

| A. | 经过0.35s时,质点Q距平衡位置的距离小于质点P距平衡位置的距离 | |
| B. | 经过0.25s时,质点Q的加速度大于质点P的加速度 | |
| C. | 经过0.15s,波沿x轴的负方向传播了3m | |
| D. | 经过0.1s时,质点Q的运动方向沿y轴正方向 |