题目内容
【题目】比萨斜塔是世界建筑史上的一大奇迹．如图所示，已知斜塔第一层离地面的高度h1=6.8m，为了测量塔的总高度，在塔顶无初速度释放一个小球，小球经过第一层到达地面的时间t1=0.2s，重力加速度g取10m/s2 ， 不计空气阻力．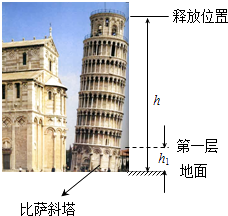
（1）求斜塔离地面的总高度h；
（2）求小球从塔顶落到地面过程中的平均速度．
【答案】
（1）解：设小球到达第一层时的速度为v1，则有
h1=v1t1+ 
得 v1= 
代入数据得v1=33m/s
塔顶离第一层的高度h2= 
=54.45m
所以塔的总高度h=h1+h2=61.25m
答：求斜塔离地面的总高度h为61.25m；
（2）小球从塔顶落到地面的总时间t= 
=3.5s
平均速度 
= 
=17.5m/s
答：小球从塔顶落到地面过程中的平均速度为17.5m/s．
【解析】（1）根据位移公式求出小球到达第一层时的速度，再求出顶离第一层的高度，进而求出总高度；（2）先求出小球从塔顶落到地面的总时间，再根据平均速度的定义求出平均速度．
【考点精析】掌握自由落体运动是解答本题的根本，需要知道（1）条件:初速度为零，只受重力作用；（2）性质:是一种初速为零的匀加速直线运动，a=g．
练习册系列答案
相关题目
