题目内容
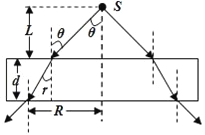
【题目】如图所示．有一个上、下表面平行且边长为a=80cm的玻璃平板，玻璃平板的折射率为n=4/3、厚度为d=12cm．现在其中心的正上方的空气中放置一点光源S，点光源距玻璃板的距离为L=18cm，从S发出的光射向玻璃板，光线与竖直方向夹角θ的最大值为53°，经过玻璃板后从下表面射出，求:玻璃板下表面未被光照亮的面积的最小值.(结果取3位小数) （sin53°=0.8）
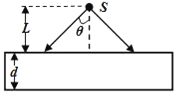
【答案】0.298m2
【解析】
作出光路图，结合折射定律求出光在上表面的折射角，根据几何关系求出玻璃板下表面圆形光斑的半径，求出玻璃板下表面未被光照亮的面积的最小值；
解：由题意可知光在玻璃板上表面发生折射时的入射角为θ，设其折射角为
，由折射定律可得：
代入数据可得：
光在玻璃板下表面发生折射时，由于入射角始终小于玻璃板的临界角，所以不会发生全反射，光在玻璃板中传播的光路图如图所示,由于是点光源，所以光从玻璃板下表面射出时形成一个圆形发光面，设其半径大小为R，则有：
代入数据可得：
其面积
玻璃板下表面未被光照亮的面积的最小值
练习册系列答案
相关题目
