题目内容
【题目】如图所示一个摆长为L=10/π2米的单摆,摆球质量为m=0.1千克,静止于平衡位置.另有质量均为m=0.1千克的小球n个与摆球在同一高度且在同一直线上,以相同的速度v=4米每秒向左运动,相邻两小球到达摆球平衡位置的时间间隔是1秒钟.每一个小球与摆球相撞后都和摆球粘在一起共同运动.(摆球和小球均视为质点,g=10m/s2)
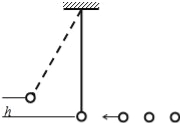
求:(1)摆球摆动的最大高度
(2)第8个小球与摆球相撞后,摆球的速度
(3)第n个小球与摆球相撞后单摆获得的动能.
【答案】(1)0.2m;(2)0;(3)见解析。
【解析】
试题分析:因为单摆的周期:T=2π![]() =2π
=2π![]() s=2s,故摆球碰撞后再回到平衡位置的时间是1s,每次摆球回到平衡位置时跟下一个小球碰撞。
s=2s,故摆球碰撞后再回到平衡位置的时间是1s,每次摆球回到平衡位置时跟下一个小球碰撞。
(1)第一个小球碰撞后,根据动量守恒定律,mv=2mv1,则有v1=![]()
以后的小球与摆球碰撞后由于质量的增加速度逐渐减小,所以摆球摆动的最大高度是第一个小球碰撞后,根据机械能守恒:2mgh=2×![]() mv12,解得:h=0.2m。
mv12,解得:h=0.2m。
(2)第二个小球与摆球碰撞后,动量守恒定律,2mv1﹣mv=3mv2,v2=0,即碰后摆球静止;
同理:第3、5、7、9…个小球碰后,摆球摆动;
第2、4、6、8…个小球碰后摆球静止
所以,第8个小球与摆球相撞后,摆球的速度是零 v8=0。
(3)第n个小球与摆球相撞后
若n为奇数:则vn﹣1=0
动量守恒定律,mv=(n+1)mvn,解得:vn=![]() ,
,
此时单摆的动能:Ek=(n+1)![]() mvn2=
mvn2=![]() mv2(n+1)=
mv2(n+1)=![]() J;
J;
若n为偶数:则:vn=0 单摆获得的动能为零。

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目