题目内容
【题目】如图所示,在离地4h的平台边缘放一个小球A,在其左侧有一个摆球B,当B球从离平台h高处由静止释放到达最低点时,恰能与A球发生正碰撞,使A球水平抛出,若A球落地时距离平台边缘4h,B球碰撞后能上升到离平台的高度![]() ,求
,求
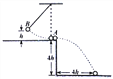
(1)碰撞后A球水平抛出时的速度.(已知重力加速度为g)
(2)A、B两球的质量之比![]() .
.
【答案】(1) ![]() (2)
(2)![]()
【解析】
(1)碰撞后A球做平抛运动,小球A在水平方向上:4h=vAt,
在竖直方向上:![]()
解得A球碰后速度为![]()
(2)设B球运动到最低点与A球碰撞前的速度为v0,碰撞后的速度大小为vB,则有:
mBgh=![]()
及mBg×![]() =
=![]()
若B球碰撞后向右运动,取向右为正方向,由动量守恒定律得:
mBv0=mB(vB)+mAvA
解得两球的质量比为:mA:mB=1:2
此条件下系统机械能损失为:△E=![]() mBgh,因碰撞过程机械能不能增加,结论合理。
mBgh,因碰撞过程机械能不能增加,结论合理。
若B球碰撞后向左运动,取向右为正方向,由动量守恒定律得:mBv0=mB(vB)+mAvA
解得两球的质量比为:mA:mB=3:2
此条件下系统机械能增加量为:△E=![]() mBgh,因碰撞过程机械能不能增加,故不合理,应舍去。
mBgh,因碰撞过程机械能不能增加,故不合理,应舍去。

练习册系列答案
相关题目