题目内容
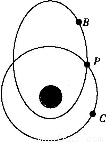
如图所示, B为绕地球做椭圆轨道运行的卫星,椭圆的半长轴 为a,运行周期为TB;C为绕地球做圆周运动的卫星,圆周的半径为r,运行周期为TC;P为B、C两卫星轨道的交点。下列说法或关系式中正确的是
A.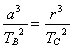 ,该比值的大小与地球质量有关
,该比值的大小与地球质量有关
B.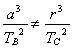 ,该比值的大小不仅仅与地球的质量有关,还有其他因素
,该比值的大小不仅仅与地球的质量有关,还有其他因素
C.卫星B在P点的加速度与卫星C在该点加速度一定相同
D.若卫星C为近地卫星,且已知C的周期和万有引力常量,则可求出地球的平均密度
【答案】
ACD
【解析】
试题分析:两颗卫星都绕同一个中心天体运动,圆周运动也是一个半长轴与半短轴等长的椭圆,所以符合开普勒第三定律,所以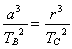 根据圆周运动万有引力提供向心力
根据圆周运动万有引力提供向心力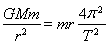 ,可得
,可得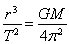 ,所以该比值只与地球质量有关,选项A对,选项B错。两颗卫星在P点距离地心距离相等,根据加速度
,所以该比值只与地球质量有关,选项A对,选项B错。两颗卫星在P点距离地心距离相等,根据加速度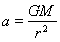 可得卫星B和卫星C在P点加速度一定相同,选项C对。若卫星C为近地卫星,则有
可得卫星B和卫星C在P点加速度一定相同,选项C对。若卫星C为近地卫星,则有 ,可得密度
,可得密度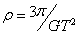 ,即可求出地球平均密度选项D对。
,即可求出地球平均密度选项D对。
考点:万有引力与航天

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
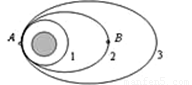
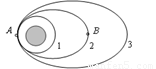
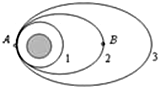 如图所示是某卫星绕地飞行的三条轨道,轨道1是近地圆形轨道,2和3是变轨后的椭圆轨道.A点是2轨道的近地点,B点是2轨道的远地点,卫星在轨道1的运行速率为7.7km/s,则下列说法中正确的是( )
如图所示是某卫星绕地飞行的三条轨道,轨道1是近地圆形轨道,2和3是变轨后的椭圆轨道.A点是2轨道的近地点,B点是2轨道的远地点,卫星在轨道1的运行速率为7.7km/s,则下列说法中正确的是( )| A、卫星在2轨道经过A点时的速率一定大于7.7km/s | B、卫星在2轨道经过B点时的速率可能大于7.7km/s | C、卫星分别在1、2轨道经过A点时的加速度相同 | D、卫星在3轨道所具有的机械能等于2轨道所具有的机械能 |
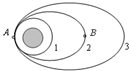 如图所示是某卫星绕地飞行的三条轨道,轨道1是近地圆形轨道,2和3是变轨后的椭圆轨道.A点是2轨道的近地点,B点是2轨道的远地点,卫星在轨道1的运行速率为7.7km/s,则下列说法中正确的是( )
如图所示是某卫星绕地飞行的三条轨道,轨道1是近地圆形轨道,2和3是变轨后的椭圆轨道.A点是2轨道的近地点,B点是2轨道的远地点,卫星在轨道1的运行速率为7.7km/s,则下列说法中正确的是( )