题目内容
在光滑水平面上有一静止的物体。现以水平恒力甲推这一物体,作用一段时间后,换成相反方向的水平恒力乙推这一物体,当恒力乙作用时间与恒力甲作用时间相同时,物体恰好回到原处,此时物体的动能为32J,则在整个过程中,恒力甲做的功等于_____________J,恒力乙做的功等于_______________J。
把32J的动能分为4份,恒力甲做的功等于32J/4 = 8J,恒力乙做的功等于24J。
解析:
解析一:本题的条件是恒力甲与恒力乙的作用时间相同,而且物体恰好回到原处。解题时要抓住这基本特征,运用牛顿运动定律和运动学公式,只要得出恒力甲与恒力乙大小之间的关系就可求得它们做功之间的关系。
解析:在恒力甲作用下,有![]()
在恒力乙作用下,有![]()
可解得:F2 = 3 F1
所以,W2 = 3 W1
把32J的动能分为4份,恒力甲做的功等于32J/4 = 8J,恒力乙做的功等于24J。
★解析二:因位移大小相等,时间间隔又相等,所以两阶段运动的平均速度大小必相等,
![]() 得
得![]()
所以
![]()
即得![]()
由动能定理得,两力做功分别为![]()
![]()
小结 此题的结论是普遍适用的,恒力甲与恒力乙之比为1:3,做功之比也为1:3,以后在电场的题中也会用到这个模型。

练习册系列答案
相关题目
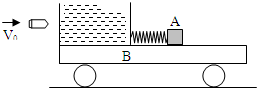 如图所示,光滑水平面上有一静止小车B,左端固定一砂箱,砂箱的右端连接一水平轻弹簧,小车与砂箱的总质量为M1=1.99kg.车上静置一物体A,其质量为M2=2.00kg.此时弹簧呈自然长度,物体A的左端的车面是光滑的,而物体A右端的车面与物体间的动摩擦因数为μ=0.2.现有一质量为m=0.01kg的子弹以水平速度v0=400m/s打入砂箱且静止在砂箱中,求:
如图所示,光滑水平面上有一静止小车B,左端固定一砂箱,砂箱的右端连接一水平轻弹簧,小车与砂箱的总质量为M1=1.99kg.车上静置一物体A,其质量为M2=2.00kg.此时弹簧呈自然长度,物体A的左端的车面是光滑的,而物体A右端的车面与物体间的动摩擦因数为μ=0.2.现有一质量为m=0.01kg的子弹以水平速度v0=400m/s打入砂箱且静止在砂箱中,求:

