题目内容
【题目】如图所示在倾角为30°的光滑斜面上，有一根直杆AB，AB长为7.5m．距A下端2.5m处有一点P．让杆由静止释放，全程杆没有脱离斜面．求：全杆经过P点所用时间（g=10m/s2）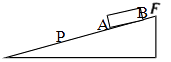
【答案】解：对杆受力分析，根据牛顿第二定律可知：mgsinθ=ma，
解得：a=5m/s2
A到达P点时有： 
，
解得： 
B点到达P点时有： 
，
解得： 
=2s
全杆经过P点所用时间为：△t=t2﹣t1=1s
答：全杆经过P点所用时间为1s
【解析】先根据牛顿第二运动定律，求出五块下滑时的加速度，再结合匀变速直线运动列方程求解。
【考点精析】根据题目的已知条件，利用匀变速直线运动的速度、位移、时间的关系的相关知识可以得到问题的答案，需要掌握速度公式：V=V0+at；位移公式：s=v0t+1/2at2；速度位移公式：vt2-v02=2as；以上各式均为矢量式，应用时应规定正方向，然后把矢量化为代数量求解，通常选初速度方向为正方向，凡是跟正方向一致的取“+”值，跟正方向相反的取“-”值．
王后雄学案教材完全解读系列答案
海淀课时新作业金榜卷系列答案
【题目】如图1所示是某同学《探究加速度与力、质量的关系》的实验装置．
（1）图2是某同学在正确操作下获得的一条纸带，A、B、C、D、E每两点之间还有4个计时点没有标出，相邻两计时点间的时间间隔为0.02s．该同学在图中标出测量的距离时，忘记写下BC和CD的数值，只标记下了AB和DE的数值．但他仍然算出了加速度的数值，则滑块的加速度大小为m/s2（结果保留两位有效数字）．
（2）通过多次实验，在保证滑块质量不变的情况下，实验中测得滑块的加速度a和细线拉力F（用沙桶和沙的总重力代替）的资料如下表所示．
F/N | 0.20 | 0.30 | 0.40 | 0.50 |
a/（m/s2） | 0.10 | 0.21 | 0.29 | 0.40 |
请你根据表中的数据在图3中作a﹣F图线．
（3）根据图线可求出滑块的质量是kg
（4）图线在F轴上截距的物理意义是 ．