Question

在粗糙水平面上放着一箱子，前面的人用与水平方向成仰角θ₁的力F₁拉箱子，同时，后面的人用与水平方向成俯角θ₂的推力F₂推箱子，此时箱子的加速度为a．如果撤去推力F₂，则箱子的加速度（　　）

A、一定增大

B、一定减小

C、可能不变

D、不是增大就是减小，不可能不变

Answer 1

分析：对箱子进行受力分析，在水平方向和竖直方向由牛顿第二定律得出方程，求出加速度，再根据μ的大小进行讨论即可求解．

解答：解：对箱子进行受力分析如图所示：

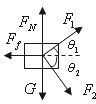
由牛顿第二定律水平方向得：
F₁cosθ₁+F₂cosθ₂-F_f=ma
竖直方向有：
F_N+F₁sinθ₁-F₂sinθ₂-mg=0
对于滑动摩擦力有：
F_f=μF_N
三式联立整理得：
a=

F1(cosθ1+μsinθ1)+F1(cosθ2-μsinθ2)

m

-μg
撤去F₂，则加速度变为a′=

F1(cosθ1+μsinθ1)

m

-μg
经过讨论可以知道，当μ＞cotθ₂时加速度变大、当μ＜cotθ₂时加速度变小、当μ=cotθ₂时加速度变不变．
故选C．

点评：本题主要考查了牛顿第二定律的直接应用，要求同学们能正确分析好物体的受力情况，难度适中．
解答去掉F₂研究加速度a的变化情况时，也可用极值法求解，即当θ₂为90°和θ₂为0°时，分析加速度的变化．