题目内容
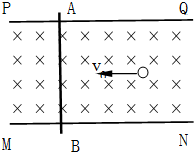 如图所示,为某一装置的俯视图,PQ、MN为竖直放置的很长的平行金属薄板,两板间有匀强磁场,它的磁感应强度大小为B,方向竖直向下,金属棒AB搁置在两板上缘,并与两板垂直良好接触,现有质量为m、带电量大小为q,其重力不计的粒子,以初速度v0水平射入两板间.问:
如图所示,为某一装置的俯视图,PQ、MN为竖直放置的很长的平行金属薄板,两板间有匀强磁场,它的磁感应强度大小为B,方向竖直向下,金属棒AB搁置在两板上缘,并与两板垂直良好接触,现有质量为m、带电量大小为q,其重力不计的粒子,以初速度v0水平射入两板间.问:(1)金属棒AB应朝什么方向、以多大的速度运动,可以使带电粒子做匀速运动?
(2)若金属棒运动突然停止,带电粒子在磁场中继续运动,从这刻开始位移第一次达到mv0/(qB)时的时间间隔是多少?(磁场足够大)
分析:(1)这又出现了带电粒子在复合场中运动时的平衡,这类题复合场中比较常见.掌握公式F电=F洛,带入有关表达式即可得到答案.
(2)明确金属棒停止后带电粒子的运动情况:金属棒停止后两板间的电场消失,只存在磁场,带电粒子在磁场中做匀速圆周运动.由洛伦兹力充当向心力可以求的轨道半径,依据半径可以求出位移大小
mv0/qB所对应的圆心角,进而可以求得时间.
(2)明确金属棒停止后带电粒子的运动情况:金属棒停止后两板间的电场消失,只存在磁场,带电粒子在磁场中做匀速圆周运动.由洛伦兹力充当向心力可以求的轨道半径,依据半径可以求出位移大小
| 3 |
解答:解:(1)不妨设粒子带正电,则f洛垂直指向MN板,F电垂直指向PQ板,故棒AB应向左运动.
由于qE=qv0B
Blv=E?l
所以有:v=v0
(2)带电粒子在匀强磁场中做匀速圆周运动,有:
qv0B=m
即:r=
当粒子位移大小第一次达到
时,可知此时粒子转过的圆心角θ=60°
则其运动时间为:t=
而T=
得:t=
答:(1)金属棒AB应向左运动、速度大小为v0可以使带电粒子做匀速运动.
(2)若金属棒运动突然停止,带电粒子在磁场中继续运动,从这刻开始位移第一次达到
时的时间间隔是
.
由于qE=qv0B
Blv=E?l
所以有:v=v0
(2)带电粒子在匀强磁场中做匀速圆周运动,有:
qv0B=m
| ||
| r |
即:r=
| mv0 |
| qB |
当粒子位移大小第一次达到
| mv0 |
| qB |
则其运动时间为:t=
| T |
| 6 |
而T=
| 2πm |
| qB |
得:t=
| πm |
| 3qB |
答:(1)金属棒AB应向左运动、速度大小为v0可以使带电粒子做匀速运动.
(2)若金属棒运动突然停止,带电粒子在磁场中继续运动,从这刻开始位移第一次达到
| mv0 |
| qB |
| πm |
| qB |
点评:第一问还好说比较简单,第二问的关键是正确分析粒子的运动轨迹.

练习册系列答案
相关题目
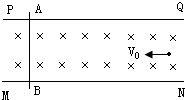 如图所示,为某一装置的俯视图,PQ、MN为竖直放置的很长的平行金属薄板,两板间有匀强磁场,它的磁感应强度大小为B,方向竖直向下,金属棒AB搁置在两板上缘,并与两板垂直良好接触,现有质量为m、带电量大小为q,其重力不计的粒子,以初速度v0水平射入两板间.问:
如图所示,为某一装置的俯视图,PQ、MN为竖直放置的很长的平行金属薄板,两板间有匀强磁场,它的磁感应强度大小为B,方向竖直向下,金属棒AB搁置在两板上缘,并与两板垂直良好接触,现有质量为m、带电量大小为q,其重力不计的粒子,以初速度v0水平射入两板间.问: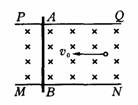

 时的时间间隔是多少?
时的时间间隔是多少?