题目内容
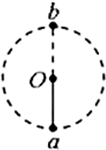 如图,细杆的一端与一小球相连,可绕过o点的水平轴自由转动,现给小球一初速度,使它在竖直平面内圆周运动,图中a、b分别表示小球轨道的最低点和最高点,则杆对球的作用力情况是( )
如图,细杆的一端与一小球相连,可绕过o点的水平轴自由转动,现给小球一初速度,使它在竖直平面内圆周运动,图中a、b分别表示小球轨道的最低点和最高点,则杆对球的作用力情况是( )| A、a处一定是拉力 | B、b处一定是拉力 | C、b处一定是支持力 | D、b处可能没有弹力 |
分析:小球在竖直平面内做圆周运动,受重力和拉力,只有重力做功,机械能守恒;在最高点和最低点重力和弹力的合力提供向心力,根据牛顿第二定律和向心力公式列式分析.
解答:解:A、在最低点a,小球受到重力和杆的弹力,合力提供向心力,向上,故杆一定是拉力,故A正确;
B、在最高点b,小球受到重力和弹力,合力提供向心力,假设弹力向下,有
F+mg=m
当v=
时,F=0,故D正确;
当v>
时,F>0,假设成立,即弹力向下,为拉力,故B错误;
当v<
时,F<0,负号表示弹力的方向与假设的方向相反,为向上的支持力,故C错误;
故选:AD.
B、在最高点b,小球受到重力和弹力,合力提供向心力,假设弹力向下,有
F+mg=m
| V2 |
| R |
当v=
| gR |
当v>
| gR |
当v<
| gR |
故选:AD.
点评:本题关键受力分析后,根据牛顿第二定律和向心力公式列式求解出杆的弹力的表达式,然后再进行讨论,注意用正负表示方向.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
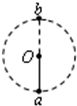 如图,细杆的一端与一小球相连,可绕过O点的水平轴自由转动,现给小球一初速度,使它在竖直平面内做圆周运动,图中a、b分别表示小球轨道的最低点和最高点,则杆对球的作用力情况是( )
如图,细杆的一端与一小球相连,可绕过O点的水平轴自由转动,现给小球一初速度,使它在竖直平面内做圆周运动,图中a、b分别表示小球轨道的最低点和最高点,则杆对球的作用力情况是( )