题目内容
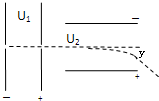 如图所示,电子在电势差为U1的加速电场中由静止开始运动,然后垂直射入电势差为U2的两板距离为d,板长为L的平行极板间的电场中,整个装置处于真空中,重力可忽略,在满足电子能射出平行板区的条件下,设电子的电量为e,质量为m.求:
如图所示,电子在电势差为U1的加速电场中由静止开始运动,然后垂直射入电势差为U2的两板距离为d,板长为L的平行极板间的电场中,整个装置处于真空中,重力可忽略,在满足电子能射出平行板区的条件下,设电子的电量为e,质量为m.求:(1)电子离开电场U1时的速度;
(2)电子在平行极板间偏移量y.
分析:(1)电子在电场U1中,电场力对电子做功为eU1,根据动能定理求解电子离开电场U1时的速度;
(2)电子进入电场U2中,做类平抛运动,水平方向做匀速直线运动,竖直方向做匀加速直线运动,根据牛顿第二定律和运动学公式结合求解y.
(2)电子进入电场U2中,做类平抛运动,水平方向做匀速直线运动,竖直方向做匀加速直线运动,根据牛顿第二定律和运动学公式结合求解y.
解答:解:(1)电子在电场U1中,根据动能定理得:
eU1=
mv2 ①
解得:v=
;
(2)在电场U2中,板间场强 E=
②
根据牛顿第二定律得:eE=ma ③
电子做类平抛运动,则有
y=
at2 ④
L=vt ⑤
联立解得:y=
;
答:
(1)电子离开电场U1时的速度为
;
(2)电子在平行极板间偏移量y为
.
eU1=
| 1 |
| 2 |
解得:v=
|
(2)在电场U2中,板间场强 E=
| U2 |
| d |
根据牛顿第二定律得:eE=ma ③
电子做类平抛运动,则有
y=
| 1 |
| 2 |
L=vt ⑤
联立解得:y=
| U2L2 |
| 4U1d |
答:
(1)电子离开电场U1时的速度为
|
(2)电子在平行极板间偏移量y为
| U2L2 |
| 4U1d |
点评:带电粒子的加速(或减速)可用动能定理求解;带电粒子的偏转可以用类平抛规律求解,注意两分运动的等时性和独立性的应用.

练习册系列答案
相关题目