题目内容
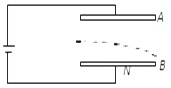 如图所示,A、B是水平放置的平行板电容器的极板,重力可以忽略不计的带电粒子以速度v0水平射入电场,且刚好沿下极板B的边缘飞出.若保持其中一个极板不动而把另一个极板移动一小段距离,粒子仍以相同的速度v0从原处飞入,则下列判断正确的是( )
如图所示,A、B是水平放置的平行板电容器的极板,重力可以忽略不计的带电粒子以速度v0水平射入电场,且刚好沿下极板B的边缘飞出.若保持其中一个极板不动而把另一个极板移动一小段距离,粒子仍以相同的速度v0从原处飞入,则下列判断正确的是( )| A、若上极板A不动,下极板B上移,粒子仍沿下极板B的边缘飞出 | B、若上极板A不动,下极板B上移,粒子将打在下板B上 | C、若下极板B不动,上极板A上移,粒子将打在下板B上 | D、若下极板B不动,上极板A上移,粒子仍沿下极板B的边缘飞出 |
分析:粒子垂直射入匀强电场中,做匀变速曲线运动,水平方向做匀速直线运动,竖直方向做初速度为零的匀加速直线运动,由牛顿第二定律和运动学公式可得到粒子偏转距离y的表达式.当极板间距离减小时,板间场强增大,极板间距离增大时,板间场强将减小,根据y的表达式分析粒子能否打在B板.
解答:解:粒子垂直射入匀强电场中,水平方向做匀速直线运动,竖直方向做初速度为零的匀加速直线运动,则得:
运动时间为 t=
偏转距离 y=
at2=
?
?(
)2=
A、B、原来粒子的偏转距离 y=
,
若上极板A不动,下极板B上移,板间距离减小.假设粒子能飞出电场,因d减小,由上式知,y>
,不可能,所以假设不成立,因此粒子不能飞出电场,打在B板上.故A错误,B正确.
C、D、若下极板B不动,上极板A上移,板间距离增大,场强减小,加速度减小,粒子必定能飞出电场,且不从B的边缘飞出,故C、D错误.
故选:B.
运动时间为 t=
| l |
| v0 |
偏转距离 y=
| 1 |
| 2 |
| 1 |
| 2 |
| qU |
| md |
| l |
| v0 |
| qUl2 |
| 2mdv02 |
A、B、原来粒子的偏转距离 y=
| d |
| 2 |
若上极板A不动,下极板B上移,板间距离减小.假设粒子能飞出电场,因d减小,由上式知,y>
| d |
| 2 |
C、D、若下极板B不动,上极板A上移,板间距离增大,场强减小,加速度减小,粒子必定能飞出电场,且不从B的边缘飞出,故C、D错误.
故选:B.
点评:本题关键能熟练运用运动的分解法,得出粒子偏转距离y的表达式,逐项分析即可求解,难度适中.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (模块3-4)如图所示,a与b是两束平行的颜色不同的单色光,它们从空气中射入水中的折射角分别为ra、rb,且ra>rb,则( )
(模块3-4)如图所示,a与b是两束平行的颜色不同的单色光,它们从空气中射入水中的折射角分别为ra、rb,且ra>rb,则( )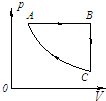
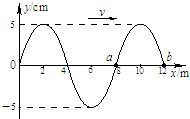
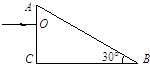
 (2010?宁河县一模)如图所示,a与b是两束平行的颜色不同的单色光,它们从空气中射入水中的折射角分别为ra、rb,且ra>rb,则( )
(2010?宁河县一模)如图所示,a与b是两束平行的颜色不同的单色光,它们从空气中射入水中的折射角分别为ra、rb,且ra>rb,则( )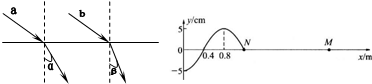
 (2006?广州二模)如图所示,a 与 b 是两束平行的颜色不同的单色光,它们从空气中射入水中的折射角分别为 ra、rb,若ra>rb,则( )
(2006?广州二模)如图所示,a 与 b 是两束平行的颜色不同的单色光,它们从空气中射入水中的折射角分别为 ra、rb,若ra>rb,则( )