��Ŀ����
8��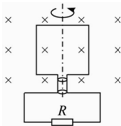 ��ͼ����Ȧ�������0.05m2����100�ѣ���Ȧ�ܵ���Ϊ1������ӵ���R=9������ǿ�ų��ĴŸ�Ӧǿ��ΪB=$\frac{1}{��}T$������Ȧ��300r/min��ת��������תʱ����
��ͼ����Ȧ�������0.05m2����100�ѣ���Ȧ�ܵ���Ϊ1������ӵ���R=9������ǿ�ų��ĴŸ�Ӧǿ��ΪB=$\frac{1}{��}T$������Ȧ��300r/min��ת��������תʱ������1��������Ȧ���������濪ʼ��ʱ��д����Ȧ�и�Ӧ�綯�Ƶ�˲ʱֵ����ʽ��
��2����·�е�ѹ������������ʾ�����Ƕ��٣�
��3���߿�ת��һ���������Ĺ�Ϊ���٣�
��4���߿��ͼʾλ��ת��30��Ĺ�����ͨ������R�ĵ���Ϊ���٣�
���� ��1������Em=nBS��������ֵ������Ȧ���������濪ʼ��ʱ��˲ʱֵΪe=Emsin��t��
��2�����ݱպϵ�·ŷķ����������������U=IR������ѹ��
��3�����ݷ����ڵ�Ÿ�Ӧ���ɹ�ʽ���綯�Ƶ�ƽ��ֵ���ٸ���ŷķ������������ƽ��ֵ��
��4������q=$\overline{I}$t���ͨ������R�ĵ�����
��� �⣺��1��n=300r/min=5r/s��
���ٶȦ�=2��n=10�У�
ת����������Ȧ�е�����Ӧ�綯��
Em=n��BS��=100��$\frac{1}{��}$��0.01��10��=10V
��Ӧ�綯�Ƶ�˲ʱ����ʽΪ
e=10sin10��t��V��
��2����Ȧ��ת�������У�������ʾ��Ϊ
I=$\frac{E}{R+r}$=$\frac{\frac{{E}_{m}}{\sqrt{2}}}{R+r}$=$\frac{10}{\sqrt{2}����9+1��}$=$\frac{\sqrt{2}}{2}$
���ѹ����ʾ��$U=IR=\frac{{\sqrt{2}}}{2}��9=4.5\sqrt{2}=6.3V$
��3��һ�����������Ĺ��������ܵ���������
��W=I2��R+r��t=��$\frac{\sqrt{2}}{2}$��2����9+1����$\frac{2��}{��}$=1J��
��4����Ȧ�������濪ʼת��90��Ĺ����У���ͨ���ı仯������=BS=0.01��$\frac{1}{��}$=$\frac{1}{��}$��10-2Wb��
����ʱ���t=$\frac{\frac{��}{2}}{2��n}$=5��10-2s
��ƽ����Ӧ�綯��Ϊ $\overline E=n\frac{����}{��t}$
����������е�ƽ������Ϊ $\overline I=\frac{\overline E}{R+r}$
ͨ���ĵ��� $q=\overline I��t$
�������ϸ�ʽ��ͨ���������ĵ���Ϊ$q=n\frac{����}{R+r}=100��\frac{{\frac{1}{��}��1{0^{-2}}}}{9+1}=\frac{1}{��}��1{0^{-1}}C$
�𣺣�1������ͼ��ʼ��ʱ����Ȧ�и�Ӧ�綯�Ƶ�˲ʱ����ʽΪe=10sin10��t��V����
��2����·�е�ѹ��ʾ��Ϊ6.3V��������ʾ����$\frac{\sqrt{2}}{2}$A��
��3�����������Ĺ�Ϊ1J��
��4����Ȧ��ͼʾλ��ת��90������У�ͨ������R�ĵ���Ϊ$\frac{1}{��}$��10-1C��
���� ����ؼ���ȷ���������ֵ����Чֵ��˲ʱֵ��ƽ��ֵ����ⷽ����ע�⽻���������������Чֵ��

 ȫ�ų��100��ϵ�д�
ȫ�ų��100��ϵ�д� Ӣ�ŵ��ϵ�д�
Ӣ�ŵ��ϵ�д�| A�� | a1=a2�����ܲ����� | B�� | a1��a2���������������� | ||
| C�� | a1��a2�������������� | D�� | a1��a2�����ܲ����� |
 ��ͼ��ʾ��ij�����ѹ����ԭ������Ȧ���������ɵ��ڣ�ԭ��Ȧ���˵�ѹΪһ���ֵ��������ҽ����磬�������������������£�Ϊ��ʹ��ѹ�����빦������ʹ��������
��ͼ��ʾ��ij�����ѹ����ԭ������Ȧ���������ɵ��ڣ�ԭ��Ȧ���˵�ѹΪһ���ֵ��������ҽ����磬�������������������£�Ϊ��ʹ��ѹ�����빦������ʹ��������| A�� | ԭ��Ȧ����n1���� | B�� | ����Ȧ����n2���� | ||
| C�� | ���ص���R����ֵ���� | D�� | ���ص���R����ֵ��С |
| A�� | 4m | B�� | 36m | C�� | 6.25m | D�� | ���ϴ𰸶����� |
| A�� | 0.7s | B�� | 0.8s | C�� | 2.4s | D�� | 2.8s |
| A�� | $\frac{5x}{2}$ | B�� | $\frac{5x}{3}$ | C�� | 2x | D�� | 3x |
 ����ŭ��С���ǰ������������õ�һ����Ϸ���õ�ǹ��һֻ����ΪM=3kg�����ˮƽ���淢�䣬��ǹ�ͷŵĵ�������ΪEP=1200J�������˶������h=20m����ߵ�ʱ������ը����Ϊ��ֻ����Ϊm=1kg��С�ֱ����ˮƽ�����ϵ���ֻС������ը֮��˲����ֻС���ٶȾ���ͬһˮƽ�������м��һֻС����ٶȺͱ�ըǰû��������ص�ʱ���뷢�䴦����ĺ���Զ��С�����Ϊd=40m��g=10m/s2�����ƿ�����������
����ŭ��С���ǰ������������õ�һ����Ϸ���õ�ǹ��һֻ����ΪM=3kg�����ˮƽ���淢�䣬��ǹ�ͷŵĵ�������ΪEP=1200J�������˶������h=20m����ߵ�ʱ������ը����Ϊ��ֻ����Ϊm=1kg��С�ֱ����ˮƽ�����ϵ���ֻС������ը֮��˲����ֻС���ٶȾ���ͬһˮƽ�������м��һֻС����ٶȺͱ�ըǰû��������ص�ʱ���뷢�䴦����ĺ���Զ��С�����Ϊd=40m��g=10m/s2�����ƿ�����������
 ��ͼ��ʾ���߳�ΪL������������abcd�ڴ�������ǿ�糡������Ϊq������ΪEk�Ĵ������ӣ�������������a����ab�������糡�����ǡ�ôӴ�c���뿪�糡��
��ͼ��ʾ���߳�ΪL������������abcd�ڴ�������ǿ�糡������Ϊq������ΪEk�Ĵ������ӣ�������������a����ab�������糡�����ǡ�ôӴ�c���뿪�糡��