题目内容
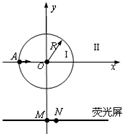
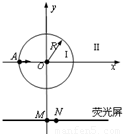
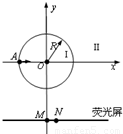
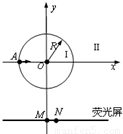
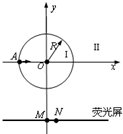 如图所示,圆心为坐标原点、半径为R的圆将xoy平面分为两个区域,即圆内区域Ⅰ和圆外区域Ⅱ.区域Ⅰ内有方向垂直于xoy平面的匀强磁场B1.平行于x轴的荧光屏垂直于xoy平面,放置在坐标y=-2.2R的位置.一束质量为m电荷量为q动能为E0的带正电粒子从坐标为(-R,0)的A点沿x轴正方向射入区域Ⅰ,当区域Ⅱ内无磁场时,粒子全部打在荧光屏上坐标为(0,-2.2R)的M点,且此时,若将荧光屏沿y轴负方向平移,粒子打在荧光屏上的位置不变.若在区域Ⅱ内加上方向垂直于xoy平面的匀强磁场B2,上述粒子仍从A点沿x轴正方向射入区域Ⅰ,则粒子全部打在荧光屏上坐标为(0.4R,-2.2R)的N点.求
如图所示,圆心为坐标原点、半径为R的圆将xoy平面分为两个区域,即圆内区域Ⅰ和圆外区域Ⅱ.区域Ⅰ内有方向垂直于xoy平面的匀强磁场B1.平行于x轴的荧光屏垂直于xoy平面,放置在坐标y=-2.2R的位置.一束质量为m电荷量为q动能为E0的带正电粒子从坐标为(-R,0)的A点沿x轴正方向射入区域Ⅰ,当区域Ⅱ内无磁场时,粒子全部打在荧光屏上坐标为(0,-2.2R)的M点,且此时,若将荧光屏沿y轴负方向平移,粒子打在荧光屏上的位置不变.若在区域Ⅱ内加上方向垂直于xoy平面的匀强磁场B2,上述粒子仍从A点沿x轴正方向射入区域Ⅰ,则粒子全部打在荧光屏上坐标为(0.4R,-2.2R)的N点.求(1)打在M点和N点的粒子运动速度v1、v2的大小.
(2)在区域Ⅰ和Ⅱ中磁感应强度B1、B2的大小和方向.
(3)若将区域Ⅱ中的磁场撤去,换成平行于x轴的匀强电场,仍从A点沿x轴正方向射入区域Ⅰ的粒子恰好也打在荧光屏上的N点,则电场的场强为多大?
分析:带电粒子在磁场中受到洛伦兹力作用下做匀速圆周运动,洛伦兹力始终与速度相垂直,因此洛伦兹力不做功,所以动能不变.带电粒子在磁场中运动,由左手定则可判定洛伦兹力方向.从而可根据运动轨迹来确定洛伦兹力的方向,最终能得出磁感应强度大小与方向.当粒子垂直射入匀强电场时,粒子做类平抛运动,从而利用平抛运动规律来解题.
解答: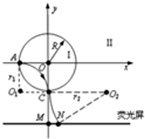 解:(1)粒子在磁场中运动时洛伦兹力不做功,打在M点和N点的粒子动能均为E0,速度v1、v2大小相等,设为v,由E0=
解:(1)粒子在磁场中运动时洛伦兹力不做功,打在M点和N点的粒子动能均为E0,速度v1、v2大小相等,设为v,由E0=
mv2可得 v=
(2)如图所示,区域Ⅱ中无磁场时,粒子在区域Ⅰ中运动四分之一圆周后,从C点沿y轴负方向打在M点,轨迹圆心是o1点,半径为r1=R
区域Ⅱ有磁场时,粒子轨迹圆心是O2点,半径为r2,
由几何关系得r22=(1.2R)2+(r2-0.4R)2
解得r2=2R
由qvB=m
得B=
故B1=
,方向垂直xoy平面向外.
B2=
,方向垂直xoy平面向里.
(3)区域Ⅱ中换成匀强电场后,粒子从C点进入电场做类平抛运动,则有1.2R=vt,
0.4R=
t2
解得场强 E=
.
 解:(1)粒子在磁场中运动时洛伦兹力不做功,打在M点和N点的粒子动能均为E0,速度v1、v2大小相等,设为v,由E0=
解:(1)粒子在磁场中运动时洛伦兹力不做功,打在M点和N点的粒子动能均为E0,速度v1、v2大小相等,设为v,由E0=| 1 |
| 2 |
|
(2)如图所示,区域Ⅱ中无磁场时,粒子在区域Ⅰ中运动四分之一圆周后,从C点沿y轴负方向打在M点,轨迹圆心是o1点,半径为r1=R
区域Ⅱ有磁场时,粒子轨迹圆心是O2点,半径为r2,
由几何关系得r22=(1.2R)2+(r2-0.4R)2
解得r2=2R
由qvB=m
| v2 |
| r |
| mv |
| qr |
故B1=
| ||
| qR |
B2=
| ||
| 2qR |
(3)区域Ⅱ中换成匀强电场后,粒子从C点进入电场做类平抛运动,则有1.2R=vt,
0.4R=
| 1 |
| 2 |
| qE |
| m |
解得场强 E=
| 10E0 |
| 9qR |
点评:带电粒子在磁场中做匀速圆周运动,处理时注意:定圆心、画轨迹、求半径;而在电场中做类平抛运动,处理时:电场强度方向做匀加速直线运动,垂直电场强度方向做匀速直线运动.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目