题目内容
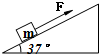如图所示，在倾角θ=37°的足够长的固定斜面上，有一质量m=1.0kg的物体，其与斜面间动摩擦因数μ=0.20．物体受到平行于斜面向上F=9.6N的拉力作用，从静止开始运动．已知sin37°=0.60，cos37°=0.80，g取10m/s2．求：（1）物体在拉力F作用下沿斜面向上运动的加速度大小；
（2）在物体的速度由0增加到2.0m/s的过程中，拉力F对物体所做的功．
分析：（1）物体向上运动的过程中，受到重力、拉力、斜面的支持力和摩擦力，将重力分解，根据牛顿第二定律求解加速度．
（2）根据公式v2-v02=2ax求出位移，再求解拉力F对物体所做的功．
（2）根据公式v2-v02=2ax求出位移，再求解拉力F对物体所做的功．
解答：解：（1）根据牛顿第二定律，得
沿斜面方向 F-Ff-mgsinθ=ma
垂直斜面方向 FN-mgcosθ=0
又Ff=μFN，得到F-μmgcosθ-mgsinθ=ma
代入解 a=2m/s2
（2）在物体的速度由0增加到2.0m/s的过程中，物体通过的位移为
x=
=1m
此过程拉力F对物体所做的功W=Fx=9.6J
答：（1）物体在拉力F作用下沿斜面向上运动的加速度大小为2m/s2．
（2）在物体的速度由0增加到2.0m/s的过程中，拉力F对物体所做的功为9.6J．
沿斜面方向 F-Ff-mgsinθ=ma
垂直斜面方向 FN-mgcosθ=0
又Ff=μFN，得到F-μmgcosθ-mgsinθ=ma
代入解 a=2m/s2
（2）在物体的速度由0增加到2.0m/s的过程中，物体通过的位移为
x=
| v2 |
| 2a |
此过程拉力F对物体所做的功W=Fx=9.6J
答：（1）物体在拉力F作用下沿斜面向上运动的加速度大小为2m/s2．
（2）在物体的速度由0增加到2.0m/s的过程中，拉力F对物体所做的功为9.6J．
点评：本题考查运用牛顿第二定律解决动力学第一类问题的能力，其基础是对物体进行受力分析．
练习册系列答案
相关题目
（2011?安徽模拟）如图所示，在倾角θ=37°的固定斜面上放置一质量M=1kg、长度L=3m的薄平板AB．平板的上表面光滑，其下端B与斜面底端C的距离为7m．在平板的上端A处放一质量m=0.6kg的滑块，开始时使平板和滑块都静止，之后将它们无初速释放．设平板与斜面间、滑块与斜面间的动摩擦因数均为μ=0.5，求滑块与平板下端B到达斜面底端C的时间差△t．（sin37°=0.6，cos37°=0.8，g=10m/s2）
（2010?南昌一模）如图所示，在倾角为a的传送带上有质量均为m的三个木块1、2，3，中间均用原长为L，劲度系数为k的轻弹簧连接起来，木块与传送带间的动摩擦因数均为μ，其中木块1被与传送带平行的细线拉住，传送带按图示方向匀速运行，三个木块处于平衡状态．下列结论正确的是（ ）
如图所示，在倾角θ=37°的斜面上，固定着宽L=0.20m的平行金属导轨，在导轨上端接有电源和滑动变阻器，已知电源电动势E=6.0V，内电阻r=0.50Ω．一根质量m=10g的金属棒ab放在导轨上，与两导轨垂直并接触良好，导轨和金属棒的电阻忽略不计．整个装置处于磁感应强度B=0.50T、垂直于轨道平面向上的匀强磁场中．若金属导轨是光滑的，已知sin37°=0.6，cos37°=0.8，取g=10m/s2，求：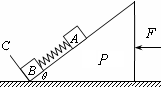
如图所示，在倾角为θ的光滑斜劈P的斜面上有两个用轻质弹簧相连的物块A、B，C为一垂直固定在斜面上的挡板．A、B质量均为m，斜面连同挡板的质量为M，弹簧的劲度系数为k，系统静止于光滑水平面．现开始用一水平恒力F作用于P，（重力加速度为g）下列说法中正确的是（ ）
如图所示，在倾角α=37°的斜面上，一条质量不计的皮带一端固定在斜面上端，另一端绕过一质量m=3kg，中间有一圈凹槽的圆柱体，并用与斜面夹角β=37°的力F拉住，使整个装置处于静止状态．不计一切摩擦，求拉力F和斜面对圆柱体的弹力N的大小． （g=10m/s2，sin37°=0.6，cos37°=0.8）