题目内容
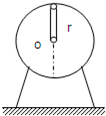 如图,在电机距轴O为r的处固定一质量为m的铁块,电机启动后,铁块以角速度ω绕O轴匀速转动,则电机对地面最大压力和最小压力之差为( )
如图,在电机距轴O为r的处固定一质量为m的铁块,电机启动后,铁块以角速度ω绕O轴匀速转动,则电机对地面最大压力和最小压力之差为( )分析:根据牛顿第二定律分别求出铁块以角速度ω绕O轴匀速转动时,在最高点和最低点转轴对铁块的作用力,从而得出电机对地面的最大压力和最小压力差.
解答:解:在最低点时,根据牛顿第二定律得,F-mg=mrω2,解得F=mg+mrω2,此时电机对地面的压力最大,N=Mg+F=Mg+mg+mrω2.
在最高点,根据牛顿第二定律得,mg+F′═mrω2,解得F′=mrω2-mg.此时电机对地面的压力最小,N′=Mg-F′=Mg+mg-mrω2.
则压力之差△F=N-N′=2mω2 r.故B正确,A、C、D错误.
故选B.
在最高点,根据牛顿第二定律得,mg+F′═mrω2,解得F′=mrω2-mg.此时电机对地面的压力最小,N′=Mg-F′=Mg+mg-mrω2.
则压力之差△F=N-N′=2mω2 r.故B正确,A、C、D错误.
故选B.
点评:解决本题的关键搞清圆周运动向心力的来源,运用牛顿第二定律进行求解.

练习册系列答案
相关题目
如图,在电机距轴O为r处固定一质量为m的铁块,电机启动后,铁块以角速度ω绕O轴匀速转动,则电机对地面最大压力和最小压力之差为:( )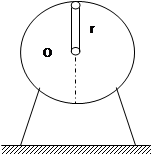
| A.2mω2 r | B.mω2 r | C.mg+2mω2 r | D.2mg+2mω2r |