题目内容
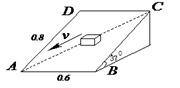
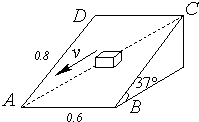 如图所示,矩形斜面水平边的长度为0.6m,倾斜边的长度为0.8m,斜面倾角为37°,一与斜面动摩擦因数为μ=0.6的小物体重25N,在与斜面平行的力F的作用下,沿对角线AC匀速下滑,求:
如图所示,矩形斜面水平边的长度为0.6m,倾斜边的长度为0.8m,斜面倾角为37°,一与斜面动摩擦因数为μ=0.6的小物体重25N,在与斜面平行的力F的作用下,沿对角线AC匀速下滑,求:(1)斜面对小物体的支持力.
(2)斜面对小物体摩擦力的大小和方向
(3)求力F的大小和方向.
(sin37°=0.6,cos37°=0.8)
分析:(1)以物体为研究对象,分析受力,将重力分解为沿斜面向下方向和垂直于斜面方向两个分力,根据平衡条件求出支持力.
(2)根据滑动摩擦力求出摩擦力.
(3)在斜面平面内,合力为零,根据平衡条件求出斜面对小物体摩擦力的大小和方向.
(2)根据滑动摩擦力求出摩擦力.
(3)在斜面平面内,合力为零,根据平衡条件求出斜面对小物体摩擦力的大小和方向.
解答: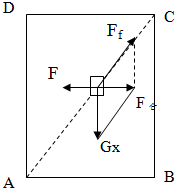 解:(1)支持力为:FN=mgcos37°=25×0.8N=20N
解:(1)支持力为:FN=mgcos37°=25×0.8N=20N
(2)滑动摩擦力方向沿AC沿斜面向上,大小为:Ff=μFN=0.6×20N=12N
(3)物体在斜面平面内受力情况如图,Gx是重力沿斜面向下的分力,Gx=Gsin37°=25×0.6N=15N,Ff=12N,由几何关系可知,Ff和Gx的合力方向与Gx垂直,有:F合=
=
N=16N
根据平衡条件得到:F=F合=16N,方向沿斜面指向BA方向
答:
(1)斜面对小物体的支持力大小为20N.
(2)斜面对小物体摩擦力的大小为12N,方向沿AC沿斜面向上.
(3)力F的大小为16N,方向沿斜面指向BA方向.
 解:(1)支持力为:FN=mgcos37°=25×0.8N=20N
解:(1)支持力为:FN=mgcos37°=25×0.8N=20N(2)滑动摩擦力方向沿AC沿斜面向上,大小为:Ff=μFN=0.6×20N=12N
(3)物体在斜面平面内受力情况如图,Gx是重力沿斜面向下的分力,Gx=Gsin37°=25×0.6N=15N,Ff=12N,由几何关系可知,Ff和Gx的合力方向与Gx垂直,有:F合=
|
| 202-122 |
根据平衡条件得到:F=F合=16N,方向沿斜面指向BA方向
答:
(1)斜面对小物体的支持力大小为20N.
(2)斜面对小物体摩擦力的大小为12N,方向沿AC沿斜面向上.
(3)力F的大小为16N,方向沿斜面指向BA方向.
点评:本题中物体的受力不在同一平面内,而是分布在立体空间内,分斜面平面和垂直于斜面平面两个平面研究,物体在任何一个平面所受的合力都为零.

练习册系列答案
相关题目
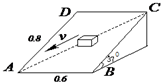 如图所示,矩形斜面水平边的长度为0.6m,倾斜边的长度为0.8m,斜面倾角为37°,一与斜面动摩擦因数为μ=0.6的小物体重25N,在与斜面平行的力F的作用下,沿对角线AC匀速下滑,求推力F.
如图所示,矩形斜面水平边的长度为0.6m,倾斜边的长度为0.8m,斜面倾角为37°,一与斜面动摩擦因数为μ=0.6的小物体重25N,在与斜面平行的力F的作用下,沿对角线AC匀速下滑,求推力F.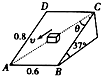 如图所示,矩形斜面水平边的长度为0.6m,倾斜边的长度为0.8m,斜面倾角为37°,一与斜面动摩擦因数为μ=0.6的小物体重25N,在与斜面平行的力F的作用下,沿对角线AC匀速下滑,求推力F的大小(Sin37°=0.6,Cos37°=0.8).
如图所示,矩形斜面水平边的长度为0.6m,倾斜边的长度为0.8m,斜面倾角为37°,一与斜面动摩擦因数为μ=0.6的小物体重25N,在与斜面平行的力F的作用下,沿对角线AC匀速下滑,求推力F的大小(Sin37°=0.6,Cos37°=0.8).