题目内容
15.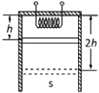 如图所示,一圆柱形绝热气缸竖竖直放置,通过绝热活塞封闭着一定质量的理想气体,活塞的质量为m,活塞的横截面积为S,初始时,气体的温度为T0,活塞与容器底部相距h,现通过电热丝缓慢加热气体,当气体吸收热Q时活塞下降h,已知大气压强为P0,重力加速度为g,不计活塞与气缸的摩擦.求此时气体的温度和加热过程中气体内能的增加量.
如图所示,一圆柱形绝热气缸竖竖直放置,通过绝热活塞封闭着一定质量的理想气体,活塞的质量为m,活塞的横截面积为S,初始时,气体的温度为T0,活塞与容器底部相距h,现通过电热丝缓慢加热气体,当气体吸收热Q时活塞下降h,已知大气压强为P0,重力加速度为g,不计活塞与气缸的摩擦.求此时气体的温度和加热过程中气体内能的增加量.
分析 (1)缓慢加热气体时气体做等压变化,确定加热前后的状态参量,根据盖吕萨克定律列方程求解;
(2)以活塞为研究对象,根据平衡条件列方程求解缸内气体压强;根据热力学第一定律求解缸内气体内能的增加量.
解答 解:(1)首先缓慢加热气体时气体做等压变化,
初状态:V1=hs T1=T0;
末状态:V2=2hs T2=?
根据盖吕萨克定律:$\frac{{V}_{1}}{{T}_{1}}$=$\frac{{V}_{2}}{{T}_{2}}$
解得:T2=2T0
(2)以活塞为研究对象受力分析,根据平衡条件:
PS+mg=P0S
得:P=P0-$\frac{mg}{S}$
气体对外做功W=P△V=(P0-$\frac{mg}{S}$)×hs
根据热力学第一定律:△U=Q-W=Q-P0hs+mgh.
答:(1)此时缸内气体的温度为2T0;
(2)加热过程中缸内气体内能的增加量Q-P0hs+mgh.
点评 解决本题的关键是:等压变化时气体做功为2=P△V.然后根据热力学第一定律计算内能的变化量.

练习册系列答案
相关题目
5.钍${\;}_{90}^{234}$Th具有放射性,它能放出一个新的粒子而变为镤${\;}_{91}^{234}$Pa,同时伴随有γ射线产生,其方程为${\;}_{90}^{234}$Th→${\;}_{91}^{234}$Pa+x,钍的半衰期为24天.则下列说法正确的是( )
| A. | x为质子 | |
| B. | x是钍核中的一个中子转化成一个质子时产生的 | |
| C. | γ射线是镤核从高能级向低能级跃迁时辐射出来的 | |
| D. | 1g钍${\;}_{90}^{234}$Th经过120天后还剩0.2g钍 |
6.火星是太阳系中唯一的类地行星,可能适合人类居住.我国计划在2020年实现火星着陆巡视,在2030年实现火星采样返回.已知火星表面的重力加速度为g火,火星的平均密度为ρ.火星可视为球体,火星探测器离火星表面的高度为h,绕火星做匀速圆周运动的周期为T.仅根据以上信息能求出的物理量是( )
| A. | 火星探测器的质量 | B. | 引力常量 | ||
| C. | 火星探测器与火星间的万有引力 | D. | 火星的第一宇宙速度 |
10. A、B两块正对的金属板竖直放置,在金属板A的内侧表面系一绝缘细线,细线下端系一带电小球(可视为点电荷).两块金属板接在如图所示的电路中,电路中的R1为光敏电阻(其阻值随所受光照强度的增大而减小),R2为滑动变阻器,R3为定值电阻.当R2的滑片P在中间时闭合电键S,此时电流表和电压表的示数分别为I和U,带电小球静止时绝缘细线与金属板A的夹角为θ.电源电动势E和内阻r一定,电表均为理想电表.下列说法中正确的是( )
A、B两块正对的金属板竖直放置,在金属板A的内侧表面系一绝缘细线,细线下端系一带电小球(可视为点电荷).两块金属板接在如图所示的电路中,电路中的R1为光敏电阻(其阻值随所受光照强度的增大而减小),R2为滑动变阻器,R3为定值电阻.当R2的滑片P在中间时闭合电键S,此时电流表和电压表的示数分别为I和U,带电小球静止时绝缘细线与金属板A的夹角为θ.电源电动势E和内阻r一定,电表均为理想电表.下列说法中正确的是( )
 A、B两块正对的金属板竖直放置,在金属板A的内侧表面系一绝缘细线,细线下端系一带电小球(可视为点电荷).两块金属板接在如图所示的电路中,电路中的R1为光敏电阻(其阻值随所受光照强度的增大而减小),R2为滑动变阻器,R3为定值电阻.当R2的滑片P在中间时闭合电键S,此时电流表和电压表的示数分别为I和U,带电小球静止时绝缘细线与金属板A的夹角为θ.电源电动势E和内阻r一定,电表均为理想电表.下列说法中正确的是( )
A、B两块正对的金属板竖直放置,在金属板A的内侧表面系一绝缘细线,细线下端系一带电小球(可视为点电荷).两块金属板接在如图所示的电路中,电路中的R1为光敏电阻(其阻值随所受光照强度的增大而减小),R2为滑动变阻器,R3为定值电阻.当R2的滑片P在中间时闭合电键S,此时电流表和电压表的示数分别为I和U,带电小球静止时绝缘细线与金属板A的夹角为θ.电源电动势E和内阻r一定,电表均为理想电表.下列说法中正确的是( )| A. | 无论将R2的滑动触头P向a端移动还是向b端移动,θ均不会变化 | |
| B. | 若将R2的滑动触头P向b端移动,则I减小,U减小 | |
| C. | 保持滑动触头P不动,用较强的光照射R1,则小球重新达到稳定后θ变小 | |
| D. | 保持滑动触头P不动,用较强的光照射R1,则U变化量的绝对值与I变化量的绝对值的比值不变 |
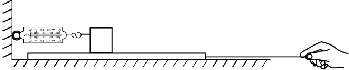
20.研究滑动摩擦力大小的实验装置如图所示,木块和木板叠放于水平桌面上,弹簧测力计水平固定,通过水平细绳与木块相连.用缓慢增大的力拉动木板,使之在桌面上滑动(木块始终未脱离木板).弹簧测力计示数稳定后,( )

| A. | 拉木板的拉力等于弹簧测力计示数 | |
| B. | 拉木板的拉力小于弹簧测力计示数 | |
| C. | 拉木板的拉力大于弹簧测力计示数 | |
| D. | 拉木板的拉力小于、等于、大于弹簧测力计示数均可 |
7.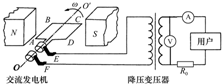 某住宅区的应急供电系统,由交流发电机和理想降压变压器组成.发电机中矩形线圈所围的面积为S,匝数为N,电阻不计.它可绕水平轴OO′在磁感应强度为B的水平匀强磁场中以角速度ω匀速转动.矩形线圈通过滑环连接变压器.R0表示输电线的电阻,其它部分电阻忽略不计.以线圈平面与磁场平行时为计时起点,下列判断正确的是( )
某住宅区的应急供电系统,由交流发电机和理想降压变压器组成.发电机中矩形线圈所围的面积为S,匝数为N,电阻不计.它可绕水平轴OO′在磁感应强度为B的水平匀强磁场中以角速度ω匀速转动.矩形线圈通过滑环连接变压器.R0表示输电线的电阻,其它部分电阻忽略不计.以线圈平面与磁场平行时为计时起点,下列判断正确的是( )
 某住宅区的应急供电系统,由交流发电机和理想降压变压器组成.发电机中矩形线圈所围的面积为S,匝数为N,电阻不计.它可绕水平轴OO′在磁感应强度为B的水平匀强磁场中以角速度ω匀速转动.矩形线圈通过滑环连接变压器.R0表示输电线的电阻,其它部分电阻忽略不计.以线圈平面与磁场平行时为计时起点,下列判断正确的是( )
某住宅区的应急供电系统,由交流发电机和理想降压变压器组成.发电机中矩形线圈所围的面积为S,匝数为N,电阻不计.它可绕水平轴OO′在磁感应强度为B的水平匀强磁场中以角速度ω匀速转动.矩形线圈通过滑环连接变压器.R0表示输电线的电阻,其它部分电阻忽略不计.以线圈平面与磁场平行时为计时起点,下列判断正确的是( )| A. | 若发电机线圈某时刻处于图示位置,变压器原线圈的电流瞬时值最小 | |
| B. | 经过半个周期,电压表读数为0 | |
| C. | 发电机线圈感应电动势的瞬时值表达式为e=NBSωsinωt | |
| D. | 当用户数目增多时,电压表的读数不变,电流表读数变大 |
4.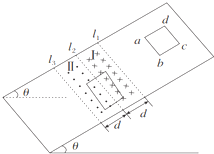 如图所示,在倾斜角为θ的光滑斜面上,相距均为d的三条虚线l1、l2、l3,它们之间的区域Ⅰ、Ⅱ分别存在垂直斜面向下和垂直斜面向上的匀强磁场,磁感应强度大小均为B,一个质量为m、边长为d、总电阻为R的正方形导线框从l1上方一定高度处由静止开始沿斜面下滑,当ab边在越过l1进入磁场Ⅰ时,恰好以速度v1做匀速直线运动;当ab边在越过l2运动到l3之前的某个时刻,线框又开始以速度v2做匀速直线运动,重力加速度为g.在线框从释放到穿出磁场的过程中,下列说法正确的是( )
如图所示,在倾斜角为θ的光滑斜面上,相距均为d的三条虚线l1、l2、l3,它们之间的区域Ⅰ、Ⅱ分别存在垂直斜面向下和垂直斜面向上的匀强磁场,磁感应强度大小均为B,一个质量为m、边长为d、总电阻为R的正方形导线框从l1上方一定高度处由静止开始沿斜面下滑,当ab边在越过l1进入磁场Ⅰ时,恰好以速度v1做匀速直线运动;当ab边在越过l2运动到l3之前的某个时刻,线框又开始以速度v2做匀速直线运动,重力加速度为g.在线框从释放到穿出磁场的过程中,下列说法正确的是( )
 如图所示,在倾斜角为θ的光滑斜面上,相距均为d的三条虚线l1、l2、l3,它们之间的区域Ⅰ、Ⅱ分别存在垂直斜面向下和垂直斜面向上的匀强磁场,磁感应强度大小均为B,一个质量为m、边长为d、总电阻为R的正方形导线框从l1上方一定高度处由静止开始沿斜面下滑,当ab边在越过l1进入磁场Ⅰ时,恰好以速度v1做匀速直线运动;当ab边在越过l2运动到l3之前的某个时刻,线框又开始以速度v2做匀速直线运动,重力加速度为g.在线框从释放到穿出磁场的过程中,下列说法正确的是( )
如图所示,在倾斜角为θ的光滑斜面上,相距均为d的三条虚线l1、l2、l3,它们之间的区域Ⅰ、Ⅱ分别存在垂直斜面向下和垂直斜面向上的匀强磁场,磁感应强度大小均为B,一个质量为m、边长为d、总电阻为R的正方形导线框从l1上方一定高度处由静止开始沿斜面下滑,当ab边在越过l1进入磁场Ⅰ时,恰好以速度v1做匀速直线运动;当ab边在越过l2运动到l3之前的某个时刻,线框又开始以速度v2做匀速直线运动,重力加速度为g.在线框从释放到穿出磁场的过程中,下列说法正确的是( )| A. | 线框中感应电流的方向不变 | |
| B. | 线框ab边从l1运动到l2所用时间大于从l2运动到l3所用时间 | |
| C. | 线框以速度v2匀速直线运动时,发热功率为$\frac{{m}^{2}{g}^{2}Rsi{n}^{2}θ}{4{B}^{2}{d}^{2}}$ | |
| D. | 线框从ab边进入磁场到速度变为v2的过程中,减少的机械能△E机与重力做功WG的关系式是△E机=WG+$\frac{1}{2}$mv${\;}_{1}^{2}$-$\frac{1}{2}$mv${\;}_{2}^{2}$ |
5.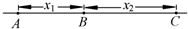 如图所示,一质点做匀加速直线运动先后经过A、B、C三点,已知从A到B和从B到C速度的增加量△v均为2m/s,AB间的距离x1=3m,BC间的距离x2=5m,则物体的加速度为( )
如图所示,一质点做匀加速直线运动先后经过A、B、C三点,已知从A到B和从B到C速度的增加量△v均为2m/s,AB间的距离x1=3m,BC间的距离x2=5m,则物体的加速度为( )
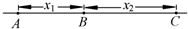 如图所示,一质点做匀加速直线运动先后经过A、B、C三点,已知从A到B和从B到C速度的增加量△v均为2m/s,AB间的距离x1=3m,BC间的距离x2=5m,则物体的加速度为( )
如图所示,一质点做匀加速直线运动先后经过A、B、C三点,已知从A到B和从B到C速度的增加量△v均为2m/s,AB间的距离x1=3m,BC间的距离x2=5m,则物体的加速度为( )| A. | 1m/s2 | B. | 2m/s2 | C. | 3m/s2 | D. | 4m/s2 |
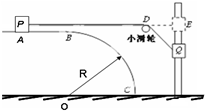 如图所示,BC为半径R=0.8m的$\frac{1}{4}$圆弧固定在水平地面上,AB为水平轨道,两轨道在B处相切连接;AB轨道上的滑块P通过不可伸长的轻绳与套在竖直光滑细杆的滑块Q连接;P、Q均可视为质点且圆弧轨道C点与竖直杆间距离足够远,开始时,P在A处,Q在与A同一水平面上的E处,且绳子刚好伸直处于水平,固定的小滑轮在D处,DE=0.35m,现把Q从静止释放,当下落h=0.35m时,P恰好到达圆弧轨道的B点,且刚好对B无压力,并且此时绳子突然断开,取g=10m/s2.试求:
如图所示,BC为半径R=0.8m的$\frac{1}{4}$圆弧固定在水平地面上,AB为水平轨道,两轨道在B处相切连接;AB轨道上的滑块P通过不可伸长的轻绳与套在竖直光滑细杆的滑块Q连接;P、Q均可视为质点且圆弧轨道C点与竖直杆间距离足够远,开始时,P在A处,Q在与A同一水平面上的E处,且绳子刚好伸直处于水平,固定的小滑轮在D处,DE=0.35m,现把Q从静止释放,当下落h=0.35m时,P恰好到达圆弧轨道的B点,且刚好对B无压力,并且此时绳子突然断开,取g=10m/s2.试求: