题目内容
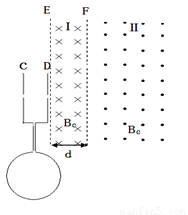
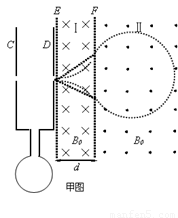
（18分）中心均开有小孔的金属板C、D与半径为d的圆形单匝金属线圈连接，圆形框内有垂直纸面的匀强磁场，大小随时间变化的关系为B=kt(k未知且k>0)，E、F为磁场边界，且与C、D板平行。D板右方分布磁场大小均为B0，方向如图所示的匀强磁场。区域Ⅰ的磁场宽度为d，区域Ⅱ的磁场宽度足够。在C板小孔附近有质量为m、电量为q的负离子由静止开始加速后，经D板小孔垂直进入磁场区域Ⅰ，不计离子重力。
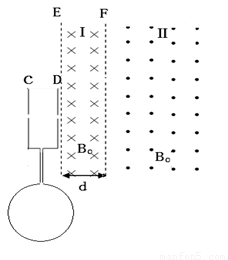
（1）判断圆形线框内的磁场方向；
（2）若离子从C板出发，运动一段时间后又恰能回到C板出发点，求离子在磁场中运动的总时间；
（3）若改变圆形框内的磁感强度变化率k，离子可从距D板小孔为2d的点穿过E边界离开磁场，求圆形框内磁感强度的变化率k是多少？
（1）圆形线框内的磁场方向垂直纸面向里;(2)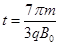 
;(3)
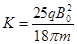
【解析】
试题分析：(1）圆形线框内的磁场方向垂直纸面向里（画在图上同样给分） (2分)
（2）离子在Ⅰ、Ⅱ区域内作圆周运动，半径均为R，有：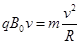
① （1分）
运动周期均为T，有：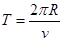
② （1分）
解①②得：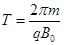
③
（1分）
由题意知粒子运动轨迹如图（甲），离子在磁场中运动的总时间为：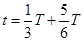
④（3分）
解③④得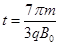： ⑤ （1分）
评分说明：只有③式，无①②式扣2分
（3）单匹圆形线框产生的电动势为U，由法拉第电磁感应定律得：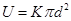
⑥
（1分）
离子从D板小孔射出速度为V，有动能定理得：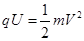
⑦ （1分）
解①⑥⑦得：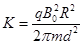
⑧ （1分）
离子进入磁场从E边界射出的运动轨迹有两种情况
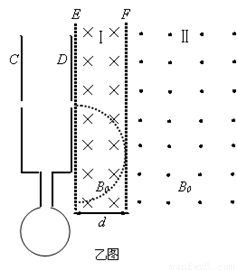
（Ⅰ）如果离子从小孔下面离开磁场，运动轨迹与F相切，如图（乙）所示
由几何关系知：R=d ⑨ （2分）
解⑧⑨得：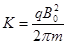
⑩
（1分）
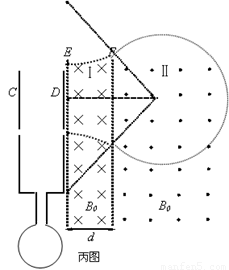
（Ⅱ）如果离子从小孔上面离开磁场，如图（丙）所示
由几何关系知：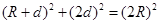
（11） （2分）
解⑧（11）得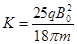： （12） （1分）
评分说明：无⑧式，答案对不扣分，无甲乙丙图不扣分。
考点：本题主要考查法拉第电磁感应定律；带电粒子在匀强磁场中的运动．
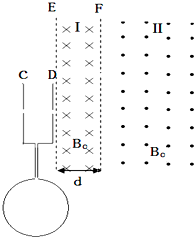（2013?惠州模拟）中心均开有小孔的金属板C、D与半径为d的圆形单匝金属线圈连接，圆形框内有垂直纸面的匀强磁场，大小随时间变化的关系为B=kt（k未知且k＞0），E、F为磁场边界，且与C、D板平行．D板右方分布磁场大小均为B0，方向如图所示的匀强磁场．区域Ⅰ的磁场宽度为d，区域Ⅱ的磁场宽度足够大．在C板小孔附近有质量为m、电量为q的负离子由静止开始加速后，经D板小孔垂直进入磁场区域Ⅰ，不计离子重力．
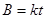(k未知且k>0)，E、F为磁场边界，且与C、D板平行。D板右方分布磁场大小均为B0，方向如图所示的匀强磁场。区域Ⅰ的磁场宽度为d，区域Ⅱ的磁场宽度足够大。在C板小孔附近有质量为m、电量为q的负离子由静止开始加速后，经D板小孔垂直进入磁场区域Ⅰ，不计离子重力。
