题目内容
10.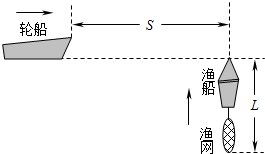 某日有雾的清晨,一艘质量为m=500t的轮船,从某码头由静止起航做直线运动,并保持发动机的输出功率等于额定功率不变,经t0=10min后,达到最大行驶速度vm=20m/s,雾也恰好散开,此时船长突然发现航线正前方S=480m处,有一只拖网渔船以v=5m/s的速度沿垂直航线方向匀速运动,且此时渔船船头恰好位于轮船的航线上,轮船船长立即下令采取制动措施,附加了恒定的制动力F=1.0×105N,结果渔船的拖网越过轮船的航线时,轮船也恰好从该点通过,从而避免了事故的发生.已知渔船连同拖网总长度L=200m(不考虑拖网渔船的宽度),假定水对船阻力的大小恒定不变,求:
某日有雾的清晨,一艘质量为m=500t的轮船,从某码头由静止起航做直线运动,并保持发动机的输出功率等于额定功率不变,经t0=10min后,达到最大行驶速度vm=20m/s,雾也恰好散开,此时船长突然发现航线正前方S=480m处,有一只拖网渔船以v=5m/s的速度沿垂直航线方向匀速运动,且此时渔船船头恰好位于轮船的航线上,轮船船长立即下令采取制动措施,附加了恒定的制动力F=1.0×105N,结果渔船的拖网越过轮船的航线时,轮船也恰好从该点通过,从而避免了事故的发生.已知渔船连同拖网总长度L=200m(不考虑拖网渔船的宽度),假定水对船阻力的大小恒定不变,求:(1)轮船减速时的加速度a;
(2)轮船的额定功率P;
(3)发现渔船时,轮船离开码头的距离.
分析 (1)先求出渔船通过的时间,轮船运动的时间等于渔船运动的时间,根据位移时间公式即可求得加速度;
(2)根据牛顿第二定律求出轮船所受阻力,最大速度行驶时,牵引力等于阻力,再根据功率P=Fvm求出功率;
(3)从开始运动到看到渔船的过程中运用动能定理即可解题
解答 解:(1)渔船通过的时间为:t=$\frac{L}{v}=\frac{200}{5}s=40s$
由运动学公式有:$s={v}_{m}t+\frac{1}{2}a{t}^{2}$,
得:$a=\frac{2(s-{v}_{m}t)}{{t}^{2}}$=-0.4m/s2
(2)轮船做减速运动时,由牛顿第二定律得:-( F+Ff)=ma
解得:Ff=1.0×105 N
最大速度行驶时,牵引力为:F=Ff=1.0×105N,
功率为:P=Fvm=Ff vm=1.0×105×20W=2.0×106 W
(3)由动能定理得:$P{t}_{0}+({F}_{f}{S}_{1})=\frac{1}{2}{mv}_{m}^{2}$
代入数据解得:S1=1.1×104m
答:(1)轮船减速时的加速度a为-0.4m/s2;
(2)轮船的额定功率P为2.0×106 W;
(3)发现渔船时,轮船离开码头的距离为1.1×104m
点评 本题主要考查了运动学基本格式、牛顿第二定律及动能定理得直接应用,难度适中,解题时注意牵引力做的功等于功率与时间的乘积

 如图所示,将小砝码置于桌面上的薄纸板上,用水平向右的拉力将纸板迅速抽出,砝码的移动很小,几乎观察不到,这就是大家熟悉的惯性演示实验,若砝码和纸板的质量分别为2m和m,各接触面间的动摩擦因数均为μ.重力加速度为g.要使纸板相对砝码运动,所需拉力的大小至少应大于( )
如图所示,将小砝码置于桌面上的薄纸板上,用水平向右的拉力将纸板迅速抽出,砝码的移动很小,几乎观察不到,这就是大家熟悉的惯性演示实验,若砝码和纸板的质量分别为2m和m,各接触面间的动摩擦因数均为μ.重力加速度为g.要使纸板相对砝码运动,所需拉力的大小至少应大于( )| A. | 3μmg | B. | 4μmg | C. | 5μmg | D. | 6μmg |
 如图所示,质量为m的木块A放在质量为M的三角形斜劈上,现用大小均为F、方向相反的水平力同时推A和B,它们均静止不动.则( )
如图所示,质量为m的木块A放在质量为M的三角形斜劈上,现用大小均为F、方向相反的水平力同时推A和B,它们均静止不动.则( )| A. | A与B之间一定存在摩擦力 | |
| B. | B与地之间可能存在摩擦力 | |
| C. | B对A的支持力一定小于mg | |
| D. | 地面对B的支持力的大小一定等于(M+m)g |
 有一理想变压器的原线圈连接一只交流电流表,副线圈接入电路的匝数可以通过滑动触头Q调节,如图所示,在副线圈两输出端连接了定值电阻R0和滑动变阻器R,在原线圈上加一电压为的交流电,则( )
有一理想变压器的原线圈连接一只交流电流表,副线圈接入电路的匝数可以通过滑动触头Q调节,如图所示,在副线圈两输出端连接了定值电阻R0和滑动变阻器R,在原线圈上加一电压为的交流电,则( )| A. | 保持Q的位置不动,将P向上滑动时,电流表的读数变大 | |
| B. | 保持Q的位置不动,将P向上滑动时,变压器的输入功率减小 | |
| C. | 保持P的位置不动,将Q向上滑动时,原、副线圈的电流比减小 | |
| D. | 保持P的位置不动,将Q向上滑动时,原、副线圈的电压比减小 |
| A. | 4 m | B. | 6 m | C. | 6.25 m | D. | 以上答案都不对 |
| A. | 在赤道上的物体线速度最大 | B. | 在两极上的物体线速度最大 | ||
| C. | 赤道上物体的角速度最大 | D. | 北京和南京的角速度大小不等 |
 如图所示,粗细均为的U形管水平部分长为L,管中盛有一定质量的液体,当U形管以加速度a向右运动时,两管内液面的高度差△h=$\frac{La}{g}$.
如图所示,粗细均为的U形管水平部分长为L,管中盛有一定质量的液体,当U形管以加速度a向右运动时,两管内液面的高度差△h=$\frac{La}{g}$. 如图,一个传送带倾斜放置,倾角α=53°,传送带的动摩擦因数为μ=0.5,长度L=10m,传送带沿顺时针方向转动,一个质量m=1kg的物体1在光滑的平台上向右做匀速直线运动,速度大小为V0,在平台末端,物体1和静止的相同质量的物体2发生弹性碰撞,碰撞后物体2水平抛出,当物体2运动到传送带上表面顶端A点时,速度方向刚好和传送带上表面平行,即物体2无碰撞地运动到传送带上,已知斜面顶端与平台的高度差h=0.8m,重力加速度g=10m/s2,sin53°=0.8,cos53°=0.6.求:
如图,一个传送带倾斜放置,倾角α=53°,传送带的动摩擦因数为μ=0.5,长度L=10m,传送带沿顺时针方向转动,一个质量m=1kg的物体1在光滑的平台上向右做匀速直线运动,速度大小为V0,在平台末端,物体1和静止的相同质量的物体2发生弹性碰撞,碰撞后物体2水平抛出,当物体2运动到传送带上表面顶端A点时,速度方向刚好和传送带上表面平行,即物体2无碰撞地运动到传送带上,已知斜面顶端与平台的高度差h=0.8m,重力加速度g=10m/s2,sin53°=0.8,cos53°=0.6.求: