题目内容
18.现有一种特殊的电池,它的电动势E约为9V,内阻r约为50Ω,已知该电池允许输出的最大电流为50mA.为了测定这个电池的电动势和内阻,某同学利用如图a所示的电路进行实验.图中电压表的内阻很大,对电路的影响可不考虑,R为电阻箱,阻值范围0~9999Ω,R0是定值电阻,起保护电路的作用.(1)实验室备有的定值电阻有以下几种规格:
A.10Ω,2.5W B.100Ω,1.0W C.200Ω,1.0W D.2000Ω,5.0W
本实验应选哪一种规格?
答:C(只需填规格的代号).
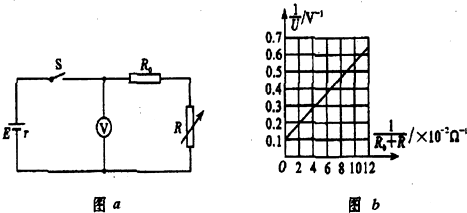
(2)该同学接入符合要求的R0后,闭合开关S,调整电阻箱的阻值,读取电压表的示数,改变电阻箱阻值,取得多组数据,作出了如图b所示的图线.则根据该同学所作出的图线可求得该电池的电动势E为10.0V,内阻r为50.0Ω.
分析 (1)已知电源电动势、内阻及最大电流,由闭合电路欧姆定律可得出电路中最小电阻,则可找出保护电阻;
(2)由闭合电路欧姆定律可得出表达式,再结合图象和数学知识可得出图象的截距及斜率的含义,则可求得电动势和内电阻.
解答 解:(1)当滑动变阻器短路时,电路中通过的最大电流为50mA,则由闭合电路欧姆定律可知,定值电阻的最小阻值为:
R0=$\frac{E}{I}$-r=$\frac{9}{0.05}$-50Ω=180-50Ω=130Ω,滑动变阻器应选C、200Ω,1.OW;
(2)由闭合电路欧姆定律可得:U=$\frac{E}{{R}_{0}+R+r}$(R0+R),
变形得:$\frac{1}{U}$=$\frac{1}{E}$+$\frac{r}{E}$$\frac{1}{{R}_{0}+R}$,
由数学知识可知,图象中的斜率k=$\frac{r}{E}$;截距b=$\frac{1}{E}$;
由图可知,b=0.1,故E=10V;
k=$\frac{0.3-0.2}{0.04-0.02}$=5,
即:$\frac{r}{E}$=5,
解得:r=50.0Ω;
故答案为:(1)C;(2)10.0;50.0.
点评 本题关键在于能由图象知识(斜率与截距的意义)结合闭合电路欧姆定律求解,在解题时要注意题目中给出的条件及坐标中隐含的信息.

练习册系列答案
相关题目
8.物理学的发展丰富了人类对物质世界的认识,推动了科学技术的创新和革命,促进了物质生产的繁荣与人类文明的进步,下列表述正确的是( )
| A. | 法拉第发现了电流的磁效应. | |
| B. | 库仑提出了库仑定律,并最早用实验测得元电荷e的数值 | |
| C. | 伽利略发现了行星运动的规律,并通过实验测出了引力常量 | |
| D. | 荷兰科学家昂尼斯(或昂纳斯)发现大多数金属在温度降到某一值时,都会出现电阻突然降为零的现象--超导现象 |
9.在如图所示电路中,电源的电动势为E,内阻为r,当变阻器R2的滑动触头P向b端移动时( )


| A. | 电压表示数变大,电流表示数变小 | B. | 电压表示数变小,电流表示数变大 | ||
| C. | 电压表示数变大,电流表示数变大 | D. | 电压表示数变小,电流表示数变小 |
6.一观察者发现,每过相等时间有一滴水自8m高的屋檐落下,而且看到当第五滴水刚要离开屋檐时,第一滴水正好落到地面,则这时第二滴水离地的高度是( )
| A. | 0.5m | B. | 2.5m | C. | 3.5m | D. | 4.5m |
13.以下对磁场认识正确的是( )
①安培分子电流假说能够解释铁棒的磁化和退磁现象
②穿过面积S的磁通量为零,则磁感应强度一定为零
③某区域中通电导线不受磁场力作用,则该区域的磁感应强度一定为零
④某点磁场方向与放在该点小磁针静止时N极的指向一致.
①安培分子电流假说能够解释铁棒的磁化和退磁现象
②穿过面积S的磁通量为零,则磁感应强度一定为零
③某区域中通电导线不受磁场力作用,则该区域的磁感应强度一定为零
④某点磁场方向与放在该点小磁针静止时N极的指向一致.
| A. | ②③ | B. | ①④ | C. | ③④ | D. | ②④ |
7. 如图所示,实线为不知方向的三条电场线,从电场中M点以相同速度飞出a、b两个带电粒子,仅在电场力作用下的运动轨迹如图中虚线所示.则( )
如图所示,实线为不知方向的三条电场线,从电场中M点以相同速度飞出a、b两个带电粒子,仅在电场力作用下的运动轨迹如图中虚线所示.则( )
 如图所示,实线为不知方向的三条电场线,从电场中M点以相同速度飞出a、b两个带电粒子,仅在电场力作用下的运动轨迹如图中虚线所示.则( )
如图所示,实线为不知方向的三条电场线,从电场中M点以相同速度飞出a、b两个带电粒子,仅在电场力作用下的运动轨迹如图中虚线所示.则( )| A. | a的速度将减小,b的速度将增加 | |
| B. | a的加速度将减小,b的加速度将增加 | |
| C. | a一定带正电,b一定带负电 | |
| D. | 两个粒子的电势能都增加 |
 一列横波沿x轴传播,传播方向未知.t时刻与t+0.4s时刻波形相同,两时刻在x轴上-3m~3m的区间内的波形如图所示.由图象可以判定
一列横波沿x轴传播,传播方向未知.t时刻与t+0.4s时刻波形相同,两时刻在x轴上-3m~3m的区间内的波形如图所示.由图象可以判定 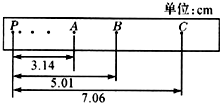 在“验证机械能守恒定律”的某次实验中,质量m=1kg的重物自由下落,在纸带上打出一系列的点,如图所示(相邻记数点时间间隔为0.02s,g取9.8m/s2,有数值计算的结果保留2位有效数字),那么:
在“验证机械能守恒定律”的某次实验中,质量m=1kg的重物自由下落,在纸带上打出一系列的点,如图所示(相邻记数点时间间隔为0.02s,g取9.8m/s2,有数值计算的结果保留2位有效数字),那么: