题目内容
18.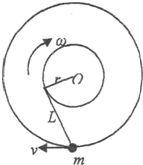 如图所示,用手握着不可伸长的细绳一端在水平桌面上做半径为r的匀速圆周运动,圆心为O,角速度为ω,细绳长为L,质量忽略不计,运动过程中细绳始终与小圆相切.在细绳的另外一端系着一个质量为m的小球,小球在桌面上恰好在以O为圆心的大圆上做圆周运动.小球和桌面之间存在摩擦力,以下说法正确的是( )
如图所示,用手握着不可伸长的细绳一端在水平桌面上做半径为r的匀速圆周运动,圆心为O,角速度为ω,细绳长为L,质量忽略不计,运动过程中细绳始终与小圆相切.在细绳的另外一端系着一个质量为m的小球,小球在桌面上恰好在以O为圆心的大圆上做圆周运动.小球和桌面之间存在摩擦力,以下说法正确的是( )| A. | 小球将做变速圆周运动 | |
| B. | 球与桌面间的动摩擦因数为$\frac{{{ω^2}r\sqrt{{r^2}+{L^2}}}}{Lg}$ | |
| C. | 细绳拉力为$m{ω^2}\sqrt{{r^2}+{L^2}}$ | |
| D. | 手对细线做功的功率为$\frac{{m{ω^3}r\sqrt{{r^2}+{L^2}}}}{L}$ |
分析 小球在水平面内做匀速圆周运动,根据小球沿着半径方向和垂直于半径方向的受力可以求得绳的拉力的大小,根据功率的公式可以求得手对细线做功的功率的大小
解答 解:A、手握着细绳做的是匀速圆周运动,所以细绳的另外一端小球随着小球做的也是匀速圆周运动,所以A错误.
B、根据摩擦力公式可得f=μmg
又:f=TsinΦ,
由于 T=$\frac{m{ω}^{2}({r}^{2}+{L}^{2})}{L}$;sinΦ=$\frac{r}{R}$=$\frac{r}{\sqrt{{r}^{2}+{L}^{2}}}$
所以,μ=$\frac{{ω}^{2}r\sqrt{{r}^{2}+{L}^{2}}}{Lg}$,所以B正确
C、设大圆为R.由图分析可知R=$\sqrt{{r}^{2}+{L}^{2}}$ ,
,
设绳中张力为T,则
TcosΦ=mRω2,
cosΦ=$\frac{L}{R}$
故T=$\frac{m{ω}^{2}{R}^{2}}{L}$=$\frac{m{ω}^{2}({r}^{2}+{L}^{2})}{L}$,所以C错误;
D、拉力的功率:P=T•V=$\frac{m{ω}^{2}{R}^{2}}{L}$•ωr=$\frac{m{ω}^{3}r({r}^{2}+{L}^{2})}{L}$,所以D错误;
故选:B
点评 小球的受力分析是本题的关键,根据小球的受力的状态分析,由平衡的条件分析即可求得小球的受力和运动的情况

练习册系列答案
相关题目
9. 在静止水面上有甲乙两艘总质量均为M的橡皮船(含乘客),甲船处于静止状态,乙船以速度v0匀速撞向甲船.如图所示,若不计水的阻力和碰撞过程中系统损失的机械能,则( )
在静止水面上有甲乙两艘总质量均为M的橡皮船(含乘客),甲船处于静止状态,乙船以速度v0匀速撞向甲船.如图所示,若不计水的阻力和碰撞过程中系统损失的机械能,则( )
 在静止水面上有甲乙两艘总质量均为M的橡皮船(含乘客),甲船处于静止状态,乙船以速度v0匀速撞向甲船.如图所示,若不计水的阻力和碰撞过程中系统损失的机械能,则( )
在静止水面上有甲乙两艘总质量均为M的橡皮船(含乘客),甲船处于静止状态,乙船以速度v0匀速撞向甲船.如图所示,若不计水的阻力和碰撞过程中系统损失的机械能,则( )| A. | 碰撞过程中乙船对甲船做的功为$\frac{1}{4}$Mv02 | |
| B. | 碰撞过程中乙船对甲船做的功为$\frac{1}{8}$Mv02 | |
| C. | 碰撞过程中两艘橡皮船具有的最大弹性势能为$\frac{1}{4}$Mv02 | |
| D. | 碰撞过程中两艘橡皮船具有的最大弹性势能为$\frac{1}{8}$Mv02 |
6.某兴趣小组设计了一个滚筒式炒栗子机器,滚筒内表面粗糙,内直径为D.工作时滚筒绕固定的水平中心轴转动.为使栗子受热均匀,要求栗子到达滚筒最高处前与筒壁脱离,则( )
| A. | 滚筒的角速度应满足ω<$\sqrt{\frac{2g}{D}}$ | |
| B. | 滚筒的角速度应满足ω>$\sqrt{\frac{2g}{D}}$ | |
| C. | 栗子脱离滚筒的位置与其质量有关 | |
| D. | 若栗子到达最高点时脱离滚筒,栗子将自由下落 |
3.关于质点,下列说法中正确的是( )
| A. | 只有体积很小的物体才能看作质点 | |
| B. | 任何静止的物体都可以看作质点 | |
| C. | 形状不规则的物体不能看作质点 | |
| D. | 研究远洋中的巨轮在海中的位置可以看作质点 |
10.在平直的高速公路上,交警发现一辆超载的货车经过某监测点,于是立即启动警车,并以4m/s2的加速度匀加速追赶前方的超载货车.问:
(1)5s末警车的速度大小是多少;
(2)5s末警车的位移大小是多少.
(1)5s末警车的速度大小是多少;
(2)5s末警车的位移大小是多少.

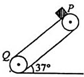 如图所示,传送带以恒定的速度v=10m/s运动,已知传送带与水平面成θ=37°角,PQ=16m,将一小物块无初速地放在传送带上P点,物块与此传送带间的动摩擦因数μ=0.5,g=lOm/s2,求:(sin37°=0.6cos37°=0.8)
如图所示,传送带以恒定的速度v=10m/s运动,已知传送带与水平面成θ=37°角,PQ=16m,将一小物块无初速地放在传送带上P点,物块与此传送带间的动摩擦因数μ=0.5,g=lOm/s2,求:(sin37°=0.6cos37°=0.8) 如图所示,质量为m的小球用长为L的细绳与O点相连,开始时小球位于A点,OA长为L,在OA的垂直平分线BC和虚线OD的交点处有一小钉,虚线OD与水平方向的夹角θ=37°,当小球由静止释放,小球运动到最低点时,细绳刚好断开(不考虑细绳与小钉碰撞的能量损失),则绳能承受的最大拉力为( )
如图所示,质量为m的小球用长为L的细绳与O点相连,开始时小球位于A点,OA长为L,在OA的垂直平分线BC和虚线OD的交点处有一小钉,虚线OD与水平方向的夹角θ=37°,当小球由静止释放,小球运动到最低点时,细绳刚好断开(不考虑细绳与小钉碰撞的能量损失),则绳能承受的最大拉力为( ) 有一个直径为L=1.5m的圆形桌子,桌面离地高度为h=1.25m.一个小物块从桌面正中心O点以初速v0=2m/s沿着桌面做直线运动最后落在水平地面上.已知动摩擦因数为μ=0.2,取g=10m/s2,求:
有一个直径为L=1.5m的圆形桌子,桌面离地高度为h=1.25m.一个小物块从桌面正中心O点以初速v0=2m/s沿着桌面做直线运动最后落在水平地面上.已知动摩擦因数为μ=0.2,取g=10m/s2,求: