题目内容
20.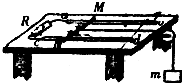 如图,在水平桌面上放置两条相距l的平行光滑导轨ab与cd,阻值为R的电阻与导轨的a、c端相连.质量为m、电阻不计的导体垂直于导轨放置并可沿导轨自由滑动.整个装置放于方向竖直向上,磁感应强度的大小为B的匀强磁场中.导体棒的中点系一不可伸长的轻绳,绳绕过固定在桌边的光滑轻滑轮后,与一个质量也为m的物块相连,用手托住物块使绳处于伸直状态.现若从静止开始释放物块,在物块下落高度h的过程中(物块不会触地),g表示重力加速度,其它电阻不计,则( )
如图,在水平桌面上放置两条相距l的平行光滑导轨ab与cd,阻值为R的电阻与导轨的a、c端相连.质量为m、电阻不计的导体垂直于导轨放置并可沿导轨自由滑动.整个装置放于方向竖直向上,磁感应强度的大小为B的匀强磁场中.导体棒的中点系一不可伸长的轻绳,绳绕过固定在桌边的光滑轻滑轮后,与一个质量也为m的物块相连,用手托住物块使绳处于伸直状态.现若从静止开始释放物块,在物块下落高度h的过程中(物块不会触地),g表示重力加速度,其它电阻不计,则( )| A. | 电阻R中的感应电流方向由a到c | |
| B. | 物体下落的最大加速度为g | |
| C. | 通过电阻R的电量为$\frac{Blh}{R}$ | |
| D. | 若h足够大,物块下落的最大速度为$\frac{mgR}{{B}^{2}{l}^{2}}$ |
分析 从静止开始释放物块,导体棒切割磁感线产生感应电流,根据右手定则判断感应电流方向.根据牛顿第二定律列式分析最大加速度.当导体棒匀速运动时,速度最大,由平衡条件和安培力的表达式结合推导出最大速度.根据感应电荷量表达式q=$\frac{△Φ}{R}$求解电量.
解答 解:A、从静止开始释放物块,导体棒切割磁感线产生感应电流,由右手定则可知,电阻R中的感应电流方向由c到a,故A错误.
B、开始时加速度最大,最大加速度a=$\frac{mg}{M+m}$;故B错误;
C、通过电阻R的电量q=$\frac{△Φ}{R}$=$\frac{B△S}{R}=\frac{Blh}{R}$.故C正确.
D、物块和滑杆先做加速运动,后做匀速运动,此时速度最大,则有mg=F,而F=BIl,I=$\frac{BLv}{R}$,解得物体下落的最大速度为v=$\frac{mgR}{{B}^{2}{l}^{2}}$.故D正确.
故选:CD
点评 本题分析物体的运动情况是解题的基础,关键掌握要会推导安培力,知道感应电荷量表达式q=$\frac{△Φ}{R}$,式中R是回路的总电阻.

练习册系列答案
相关题目
11.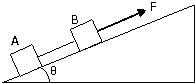 如图8所示,分别为mA、mB的A、B两物块用轻线连接放在倾角为θ的斜面上,用始终平行于斜面向上的恒定拉力F拉A,使A、B沿斜面向上一起做匀加速运动,A、B与斜面的动摩擦因数均为μ,为了增大细线上的张力,下列办法可行的是( )
如图8所示,分别为mA、mB的A、B两物块用轻线连接放在倾角为θ的斜面上,用始终平行于斜面向上的恒定拉力F拉A,使A、B沿斜面向上一起做匀加速运动,A、B与斜面的动摩擦因数均为μ,为了增大细线上的张力,下列办法可行的是( )
 如图8所示,分别为mA、mB的A、B两物块用轻线连接放在倾角为θ的斜面上,用始终平行于斜面向上的恒定拉力F拉A,使A、B沿斜面向上一起做匀加速运动,A、B与斜面的动摩擦因数均为μ,为了增大细线上的张力,下列办法可行的是( )
如图8所示,分别为mA、mB的A、B两物块用轻线连接放在倾角为θ的斜面上,用始终平行于斜面向上的恒定拉力F拉A,使A、B沿斜面向上一起做匀加速运动,A、B与斜面的动摩擦因数均为μ,为了增大细线上的张力,下列办法可行的是( )| A. | 仅增大A的质量mA | B. | 仅增大B的质量mB | ||
| C. | 仅增大斜面倾角θ(F仍平行于斜面) | D. | 仅增大动摩擦因数μ |
15.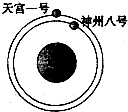 2011年11月1日,我国成功发射“神州八号”飞船,“神州八号”飞船在入轨后两天,与“天宫一号”目标飞行器成功进行交会对接.假如“神州八号”与“天宫一号”对接前所处的轨道如图所示,下列说法正确的是( )
2011年11月1日,我国成功发射“神州八号”飞船,“神州八号”飞船在入轨后两天,与“天宫一号”目标飞行器成功进行交会对接.假如“神州八号”与“天宫一号”对接前所处的轨道如图所示,下列说法正确的是( )
 2011年11月1日,我国成功发射“神州八号”飞船,“神州八号”飞船在入轨后两天,与“天宫一号”目标飞行器成功进行交会对接.假如“神州八号”与“天宫一号”对接前所处的轨道如图所示,下列说法正确的是( )
2011年11月1日,我国成功发射“神州八号”飞船,“神州八号”飞船在入轨后两天,与“天宫一号”目标飞行器成功进行交会对接.假如“神州八号”与“天宫一号”对接前所处的轨道如图所示,下列说法正确的是( )| A. | “天宫一号”的加速度比“神州八号”的大 | |
| B. | “天宫一号”的运行周期比“神州八号”的长 | |
| C. | “神州八号”适当加速后才能与“天宫一号”实现对接 | |
| D. | “神州八号”从图示轨道运动到“天宫一号”对接的过程中,动能增加 |
12. 如图所示,一个金属圆盘安装在竖直的转动轴上,置于蹄形磁铁之间,两块铜片A、O分别与金属盘的边缘和转动轴接触.若使金属盘按图示方向(俯视顺时针方向)转动起来,下列说法正确的是( )
如图所示,一个金属圆盘安装在竖直的转动轴上,置于蹄形磁铁之间,两块铜片A、O分别与金属盘的边缘和转动轴接触.若使金属盘按图示方向(俯视顺时针方向)转动起来,下列说法正确的是( )
 如图所示,一个金属圆盘安装在竖直的转动轴上,置于蹄形磁铁之间,两块铜片A、O分别与金属盘的边缘和转动轴接触.若使金属盘按图示方向(俯视顺时针方向)转动起来,下列说法正确的是( )
如图所示,一个金属圆盘安装在竖直的转动轴上,置于蹄形磁铁之间,两块铜片A、O分别与金属盘的边缘和转动轴接触.若使金属盘按图示方向(俯视顺时针方向)转动起来,下列说法正确的是( )| A. | 电阻R中有Q→R→P方向的感应电流 | |
| B. | 电阻R中有P→R→Q方向的感应电流 | |
| C. | 穿过圆盘的磁通量始终没有变化,电阻R中无感应电流 | |
| D. | 调换磁铁的N、S极同时改变金属盘的转动方向,R中感应电流的方向也会发生改变 |
9.一简谐波在如图所示的x轴上传播,实线和虚线分别是t1=0和t2=0.2s时刻的波形图.则( )

| A. | 若该波的传播速度是75m/s,则该波沿-x方向传播 | |
| B. | 若该波与另一频率为1.25Hz的简谐波相遇时发生干涉,则该波沿+x方向传播 | |
| C. | 若该波在t1=0.2s时刻,x=2.5m处的质点向-y方向运动,则该波向+x方向传播 | |
| D. | 若该波在t1=0时刻已沿+x方向恰传播到x=6m处,则波源起振方向向下 |
10.双星也是一种天文现象;将两颗距离较近,且相互绕行的天体称为双星,已知双星A、B的质量分别为m1和m2,它们之间的距离为L,G为万有引力常量,A、B均可视为质点,则( )
| A. | A、B的角速度之比为m1:m2 | B. | A、B所受的向心力之比为m1:m2 | ||
| C. | B的半径为$\frac{{m}_{1}L}{{m}_{1}+{m}_{2}}$ | D. | B的向心加速度大小为$\frac{G{m}_{1}}{{L}^{2}}$ |
 如图所示,若放置在桌面上的线圈匝数为100匝,当竖立的条形磁铁在线圈中心上方某一高度时,线圈内的磁通量为0.01Wb,现把条形磁铁插入线圈内,当磁铁停止在线圈内的桌面上时,线圈内的磁通量为0.07Wb.问:
如图所示,若放置在桌面上的线圈匝数为100匝,当竖立的条形磁铁在线圈中心上方某一高度时,线圈内的磁通量为0.01Wb,现把条形磁铁插入线圈内,当磁铁停止在线圈内的桌面上时,线圈内的磁通量为0.07Wb.问: 如图所示,传送带与地面成夹角θ=37°,以10m/s的速度逆时针转动,在传送带上端轻轻地放一个质量m=1kg的物体,它与传送带间的动摩擦因数μ=0.5.已知传送带从A到B的长度L=29m,g取10m/s2,sin37°=0.6,cos37°=0.8,求:
如图所示,传送带与地面成夹角θ=37°,以10m/s的速度逆时针转动,在传送带上端轻轻地放一个质量m=1kg的物体,它与传送带间的动摩擦因数μ=0.5.已知传送带从A到B的长度L=29m,g取10m/s2,sin37°=0.6,cos37°=0.8,求: