题目内容
一列横波在x轴上传播,t1=0和t2="0.005" s时的波形,如图所示的实线和虚线.

(1)设周期大于(t2-t1),求波速.
(2)设周期小于(t2-t1),并且波速为6000 m/s.求波的传播方向.

(1)设周期大于(t2-t1),求波速.
(2)设周期小于(t2-t1),并且波速为6000 m/s.求波的传播方向.
(1)若波沿x轴正向,v=400 m/s
若波沿x轴负向,v=1200 m/s
(2)沿x轴负向
若波沿x轴负向,v=1200 m/s
(2)沿x轴负向
当波传播时间小于周期时,波沿传播方向前进的距离小于一个波长,当波传播的时间大于周期时,波沿传播方向前进的距离大于波长.这时从波形的变化上看出的传播距离加上n个波长才是波实际传播的距离.
(1)因Δt=(t2-t1)<T,所以波传播的距离可以直接由图读出.
若波沿+x方向传播,则在0.005 s内传播了2 m,故波速为
v=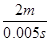 =400 m/s,
=400 m/s,
若波沿-x方向传播,则在0.005 s内传播了6 m,故波速为
v=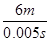 =1200 m/s.
=1200 m/s.
(2)因(t2-t1)>T,所以波传播的距离大于一个波长,在0.005 s内传播的距离为
Δx="vt=6000×0.005" m="30" m,
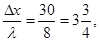 即Δx=3λ+
即Δx=3λ+ λ.
λ.
因此,可得波的传播方向沿x轴的负方向.
(1)因Δt=(t2-t1)<T,所以波传播的距离可以直接由图读出.
若波沿+x方向传播,则在0.005 s内传播了2 m,故波速为
v=
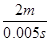 =400 m/s,
=400 m/s,若波沿-x方向传播,则在0.005 s内传播了6 m,故波速为
v=
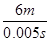 =1200 m/s.
=1200 m/s.(2)因(t2-t1)>T,所以波传播的距离大于一个波长,在0.005 s内传播的距离为
Δx="vt=6000×0.005" m="30" m,
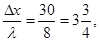 即Δx=3λ+
即Δx=3λ+ λ.
λ.因此,可得波的传播方向沿x轴的负方向.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目




 ,b点振动减弱
,b点振动减弱 的两个焦点F1和F2上放置两个频率相同的波源,它们激起的波的波长为4cm。关于图中A、B、C、D四个质点的振动情况,下列说法中正确的是
的两个焦点F1和F2上放置两个频率相同的波源,它们激起的波的波长为4cm。关于图中A、B、C、D四个质点的振动情况,下列说法中正确的是