题目内容
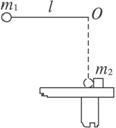
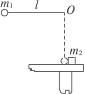
如图
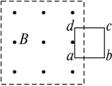
图
(1)当两船相遇时,两船各行进了多少米?
(2)当两船相遇不相碰的瞬间,为了避免碰撞,人从甲船跳向乙船需要对地的最小水平速度为
解析:(1)由动量守恒定律,得(m甲+m人)v甲=m乙v乙
有(m甲+m人)s甲=m乙s乙
s甲+s乙=
(2)为了避免碰撞,人跳到乙船后系统至少要静止.设人在起跳前瞬间甲船和人的速度为v1,乙船速度为v2,对甲船和人组成的系统由动量守恒得,(m甲+m人)v1=m人×
得v1=
解得F=90 N.
答案:(1)

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目