题目内容
【题目】竖直平面内半径为R的光滑圆弧轨道CDM与左侧光滑斜面体ABC相切于C点,倾角分别如图所示。O为圆弧圆心,D为圆弧最低点,C、M在同一水平高度。斜面体ABC固定在地面上,顶端B安装一个光滑的定滑轮,一轻质细绳跨过定滑轮分别连接小物块P、Q(两边细绳分别与对应斜面平行),此时P、Q两物块在斜面上保持静止。若PC间距L1=0.25 m,物块P质量m1=3 kg。(取g=10 m/s2。sin 37°=0.6,cos 37°=0.8)求:
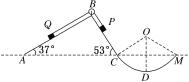
(1)小物块Q的质量m2;
(2)若烧断细绳后,物块P第一次过D点时对轨道的压力大小为78 N,则圆弧面的半径R是多少?
【答案】(1) 4 kg (2) 0.5 m
【解析】
(1)P、Q两物块在斜面上保持静止,根据平衡条件得:
对P受力m1gsin 53°=T ①
对Q受力T=m2gsin 37° ②
由①②式代入数据解得:m2=4 kg。
(2)物块P运动到D过程由机械能守恒定律得:m1gh=![]() m1vD2 ③
m1vD2 ③
由几何关系得:h=L1sin 53°+R(1-cos 53°) ④
物块P运动到D点时,根据牛顿第二定律:FD-m1g=m1![]() ⑤
⑤
由③④⑤代入数据得:R=0.5 m。

练习册系列答案
相关题目