题目内容
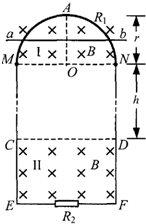 (2008?上海)如图所示,竖直平面内有一半径为r、内阻为R1、粗细均匀的光滑半圆形金属球,在M、N处与相距为2r、电阻不计的平行光滑金属轨道ME、NF相接,EF之间接有电阻R2,已知R1=12R,R2=4R.在MN上方及CD下方有水平方向的匀强磁场I和II,磁感应强度大小均为B.现有质量为m、电阻不计的导体棒ab,从半圆环的最高点A处由静止下落,在下落过程中导体棒始终保持水平,与半圆形金属环及轨道接触良好,高平行轨道中够长.已知导体棒ab下落r/2时的速度大小为v1,下落到MN处的速度大小为v2.
(2008?上海)如图所示,竖直平面内有一半径为r、内阻为R1、粗细均匀的光滑半圆形金属球,在M、N处与相距为2r、电阻不计的平行光滑金属轨道ME、NF相接,EF之间接有电阻R2,已知R1=12R,R2=4R.在MN上方及CD下方有水平方向的匀强磁场I和II,磁感应强度大小均为B.现有质量为m、电阻不计的导体棒ab,从半圆环的最高点A处由静止下落,在下落过程中导体棒始终保持水平,与半圆形金属环及轨道接触良好,高平行轨道中够长.已知导体棒ab下落r/2时的速度大小为v1,下落到MN处的速度大小为v2.(1)求导体棒ab从A下落r/2时的加速度大小.
(2)若导体棒ab进入磁场II后棒中电流大小始终不变,求磁场I和II之间的距离h和R2上的电功率P2.
(3)若将磁场II的CD边界略微下移,导体棒ab刚进入磁场II时速度大小为v3,要使其在外力F作用下做匀加速直线运动,加速度大小为a,求所加外力F随时间变化的关系式.
分析:(1)导体棒受到重力和安培力的作用,注意此时导体棒的有效切割长度和外电路的串并联情况.
(2)导体棒ab进入磁场II后棒中电流大小始终不变,说明导体棒匀速运动,导体棒在下落h的过程中做匀变速直线运动,根据运动规律可求出下落距离h,根据并联电路可知R2上消耗的功率占整个电路的
,总电功率等于导体棒重力功率.
(3)正确进行受力分析,注意安培力的表达式,然后根据牛顿第二定律求解即可.
(2)导体棒ab进入磁场II后棒中电流大小始终不变,说明导体棒匀速运动,导体棒在下落h的过程中做匀变速直线运动,根据运动规律可求出下落距离h,根据并联电路可知R2上消耗的功率占整个电路的
| 3 |
| 4 |
(3)正确进行受力分析,注意安培力的表达式,然后根据牛顿第二定律求解即可.
解答:解:(1)以导体棒为研究对象,棒在磁场I中切割磁感线,棒中产生产生感应电动势,导体棒ab从A下落
时,导体棒在重力与安培力作用下做加速运动,由牛顿第二定律,得:
mg-BIL=ma,式中l=
r,I=
式中:R总=
=4R
由以上各式可得到:a=g-
故导体棒ab从A下落
时的加速度大小为:a=g-
.
(2)当导体棒ab通过磁场II时,若安培力恰好等于重力,棒中电流大小始终不变,即:mg=BI×2r=B×
×2r=
式中:R并=
=3R
解得:vt=
=
导体棒从MN到CD做加速度为g的匀加速直线运动,有vt2-v22=2gh,
得:h=
-
,
此时导体棒重力的功率为:PG=mgvt=
,
根据能量守恒定律,此时导体棒重力的功率全部转化为电路中的电功率,即P电=P1+P2=PG=
,
所以,P2=
PG=
,
故磁场I和II之间的距离h=
-
,和R2上的电功率P2=
.
(3)设导体棒ab进入磁场II后经过时间t的速度大小为v't,此时安培力大小为:F′=
由于导体棒ab做匀加速直线运动,有v't=v3+at
根据牛顿第二定律,有
F+mg-F′=ma
即:F+mg-
=ma
由以上各式解得:F=
(at+v3)-m(g-a)=
t+
+ma-mg
故所加外力F随时间变化的关系式为:F=
t+
+ma-mg.
| r |
| 2 |
mg-BIL=ma,式中l=
| 3 |
| Blv1 |
| R总 |
式中:R总=
| 8R×(4R+4R) |
| 8R+(4R+4R) |
由以上各式可得到:a=g-
| 3B2r2v1 |
| 4mR |
故导体棒ab从A下落
| r |
| 2 |
| 3B2r2v1 |
| 4mR |
(2)当导体棒ab通过磁场II时,若安培力恰好等于重力,棒中电流大小始终不变,即:mg=BI×2r=B×
| B×2r×vt |
| R并 |
| 4B2r2vt |
| R并 |
式中:R并=
| 12R×4R |
| 12R+4R |
解得:vt=
| mgR并 |
| 4B2r2 |
| 3mgR |
| 4B2r2 |
导体棒从MN到CD做加速度为g的匀加速直线运动,有vt2-v22=2gh,
得:h=
| 9m2gr2 |
| 32B4r4 |
| ||
| 2g |
此时导体棒重力的功率为:PG=mgvt=
| 3m2g2R |
| 4B2r2 |
根据能量守恒定律,此时导体棒重力的功率全部转化为电路中的电功率,即P电=P1+P2=PG=
| 3m2g2R |
| 4B2r2 |
所以,P2=
| 3 |
| 4 |
| 9m2g2R |
| 16B2r2 |
故磁场I和II之间的距离h=
| 9m2gr2 |
| 32B4r4 |
| ||
| 2g |
| 9m2g2R |
| 16B2r2 |
(3)设导体棒ab进入磁场II后经过时间t的速度大小为v't,此时安培力大小为:F′=
| 4B2r2v′t |
| 3R |
由于导体棒ab做匀加速直线运动,有v't=v3+at
根据牛顿第二定律,有
F+mg-F′=ma
即:F+mg-
| 4B2r2(v3+at) |
| 3R |
由以上各式解得:F=
| 4B2r2 |
| 3R |
| 4B2r2a |
| 3R |
| 4B2r2v3 |
| 3R |
故所加外力F随时间变化的关系式为:F=
| 4B2r2a |
| 3R |
| 4B2r2v3 |
| 3R |
点评:本题考查了关于电磁感应的复杂问题,对于这类问题一定要做好电流、安培力、运动情况、功能关系这四个方面的问题分析.

练习册系列答案
相关题目
 (2008?上海)如图所示,两端开口的弯管,左管插入水银槽中,右管有一段高为h的水银柱,中间封有一段空气,则( )
(2008?上海)如图所示,两端开口的弯管,左管插入水银槽中,右管有一段高为h的水银柱,中间封有一段空气,则( ) (2008?上海)如图所示,在竖直平面内的直角坐标系中,一个质量为m的质点在外力F的作用下,从坐标原点O由静止沿直线ON斜向下运动,直线ON与y轴负方向成θ角(θ<π/4).则F大小至少为
(2008?上海)如图所示,在竖直平面内的直角坐标系中,一个质量为m的质点在外力F的作用下,从坐标原点O由静止沿直线ON斜向下运动,直线ON与y轴负方向成θ角(θ<π/4).则F大小至少为 (2008?上海)如图所示,把电量为-5×10-9C的电荷,从电场中的A点移到B点,其电势能
(2008?上海)如图所示,把电量为-5×10-9C的电荷,从电场中的A点移到B点,其电势能 (2008?上海)如图所示,一根木棒AB在O点被悬挂起来,已知AO=OC,在A、C两点分别挂有2个和3个质量相等的砝码,木棒处于平衡状态.现在木棒的A、C点各增加3个同样的砝码,关于木棒的运动状态下列说法正确的是( )
(2008?上海)如图所示,一根木棒AB在O点被悬挂起来,已知AO=OC,在A、C两点分别挂有2个和3个质量相等的砝码,木棒处于平衡状态.现在木棒的A、C点各增加3个同样的砝码,关于木棒的运动状态下列说法正确的是( ) (2008?上海)如图所示,用导线将验电器与洁净锌板连接,触摸锌板使验电器指示归零.用紫外线照射锌板,验电器指针发生明显偏转,接着用毛皮摩擦过的橡胶棒接触锌板,发现验电器指针张角减小,此现象说明锌板带
(2008?上海)如图所示,用导线将验电器与洁净锌板连接,触摸锌板使验电器指示归零.用紫外线照射锌板,验电器指针发生明显偏转,接着用毛皮摩擦过的橡胶棒接触锌板,发现验电器指针张角减小,此现象说明锌板带