题目内容
15.作匀减速直线运动的物体,依次通过A、B、C三点,位移SAB=3SBC,已知物体在AB段的平均速度大小为12m/s,在BC段的平均速度大小为6m/s,那么物体在B点时的瞬时速度的大小为( )| A. | 8m/s | B. | 8.4m/s | C. | 9m/s | D. | 9.6m/s |
分析 物体做匀加速直线运动,对AB、BC两段过程分别根据速度位移关系式列方程,得出A、B、C三点的速度与位移的关系,根据AB段和BC段的平均速度与A、B、C三点的速度列式,联立求出vB.
解答 解:设加速度大小为a,经A、B、C的速度大小分别为vA、vB、vC.SBC=L.
据匀加速直线运动规律可得:
vB2-vA2=2a•3L
vC2-vB2=2aL
$\frac{{v}_{A}+{v}_{B}}{2}={v}_{1}$=12m/s
$\frac{{v}_{C}+{v}_{B}}{2}={v}_{2}$=6m/s
联立可得:vB=8.4m/s
故选:B.
点评 本题关键要充分运用好条件:ab、bc的距离相等,以及两段的平均速度,灵活运用运动学公式求解.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
5.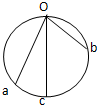 如图所示,O点是竖直圆环的顶点,Oc是圆环的直径,Oa和Ob是两条不同倾角的弦.在Oa、Ob、Oc线上置三个光滑的斜面,一质点自O点自由释放,先后分别沿Oa、Ob、Oc下滑,到圆环上的三点时间比较( )
如图所示,O点是竖直圆环的顶点,Oc是圆环的直径,Oa和Ob是两条不同倾角的弦.在Oa、Ob、Oc线上置三个光滑的斜面,一质点自O点自由释放,先后分别沿Oa、Ob、Oc下滑,到圆环上的三点时间比较( )
 如图所示,O点是竖直圆环的顶点,Oc是圆环的直径,Oa和Ob是两条不同倾角的弦.在Oa、Ob、Oc线上置三个光滑的斜面,一质点自O点自由释放,先后分别沿Oa、Ob、Oc下滑,到圆环上的三点时间比较( )
如图所示,O点是竖直圆环的顶点,Oc是圆环的直径,Oa和Ob是两条不同倾角的弦.在Oa、Ob、Oc线上置三个光滑的斜面,一质点自O点自由释放,先后分别沿Oa、Ob、Oc下滑,到圆环上的三点时间比较( )| A. | 到a点所用的时间最短 | B. | 到b点所用的时间最短 | ||
| C. | 到c点所用的时间最短 | D. | 到a、b、c三点所用的时间一样长 |
12.银河系中的星系多为只有一颗或两颗恒星的单星系或双星系,具有三颗以上恒星的星系被称为聚星系,近年来,也有聚星系陆续被观测到.聚星系的动力学问题很复杂,现在,我们假设有一种较简单的三星系统,三颗恒星质量相等,处在一个正三角形的三个顶点上,它们仅在彼此的引力作用下绕着正三角形的中心做匀速圆周运动,周期为T,已知它们之间的距离为r,它们自身的大小与它们之间的距离相比可以忽略.万有引力常量为G,则可以推知每颗恒星的质量为( )
| A. | $\frac{{4{π^2}{r^3}}}{{G{T^2}}}$ | B. | $\frac{{4{π^2}{r^3}}}{{3G{T^2}}}$ | C. | $\frac{{4\sqrt{3}{π^2}{r^3}}}{{3G{T^2}}}$ | D. | $\frac{{2{π^2}{r^3}}}{{G{T^2}}}$ |
10. 如图所示,用细绳系住小球放在倾角为θ的光滑斜面上,当细绳由水平方向逐渐向上偏移时,球对绳的拉力F和对斜面的压力N将( )
如图所示,用细绳系住小球放在倾角为θ的光滑斜面上,当细绳由水平方向逐渐向上偏移时,球对绳的拉力F和对斜面的压力N将( )
 如图所示,用细绳系住小球放在倾角为θ的光滑斜面上,当细绳由水平方向逐渐向上偏移时,球对绳的拉力F和对斜面的压力N将( )
如图所示,用细绳系住小球放在倾角为θ的光滑斜面上,当细绳由水平方向逐渐向上偏移时,球对绳的拉力F和对斜面的压力N将( )| A. | F逐渐增大,N逐渐减小 | B. | F逐渐减小,N逐渐增大 | ||
| C. | F先增大后减小,N逐渐减小 | D. | F先减小后增大,N逐渐减小 |
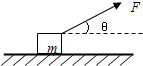 一个质量为m的物体,静止于水平面上,物体与水平面间的动摩擦因数为μ,现用与水平方向成θ角的力F斜向上拉物体,如图,已知重力加速度为g,则
一个质量为m的物体,静止于水平面上,物体与水平面间的动摩擦因数为μ,现用与水平方向成θ角的力F斜向上拉物体,如图,已知重力加速度为g,则
 如图所示,木工常用木楔来固定木榫,直角三角形楔子底边长l=35mm,高h=12mm,今用水平力F打入楔子时,木楔自身重力不计,摩擦不计,求:
如图所示,木工常用木楔来固定木榫,直角三角形楔子底边长l=35mm,高h=12mm,今用水平力F打入楔子时,木楔自身重力不计,摩擦不计,求: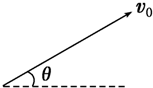 质量为m、电荷量为+q的小球以初速度v0以与水平方向成θ角射出,如图所示,如果在某方向加上一定大小的匀强电场后,能保证小球仍沿v0方向做直线运动,试求所加匀强电场的最小值,加了这个电场后,经多长时间速度变为零?
质量为m、电荷量为+q的小球以初速度v0以与水平方向成θ角射出,如图所示,如果在某方向加上一定大小的匀强电场后,能保证小球仍沿v0方向做直线运动,试求所加匀强电场的最小值,加了这个电场后,经多长时间速度变为零?