题目内容
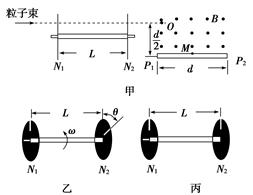
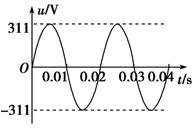
(2010年高考广东理综卷)如图甲所示,左为某同学设想的粒子速度选择装置,由水平转轴及两个薄盘N1、N2构成,两盘面平行且与转轴垂直,相距为L,盘上各开一狭缝,两狭缝夹角θ可调(如图乙);右为水平放置的长为d的感光板,板的正上方有一匀强磁场,方向垂直纸面向外,磁感应强度为B.一小束速度不同、带正电的粒子沿水平方向射入N1,能通过N2的粒子经O点垂直进入磁场,O到感光板的距离为 ,粒子电荷量为q,质量为m,不计重力.
,粒子电荷量为q,质量为m,不计重力.

(1)若两狭缝平行且盘静止(如图丙),某一粒子进入磁场后,竖直向下打在感光板中心点M上,求该粒子在磁场中运动的时间t;
(2)若两狭缝夹角为θ0,盘匀速转动,转动方向如图乙,要使穿过N1、N2的粒子均打到感光板P1P2连线上,试分析盘转动角速度ω的取值范围.(设通过N1的所有粒子在盘旋转一圈的时间内都能到达N2)
(1) 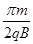 (2)
(2) 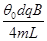 ≤ω≤
≤ω≤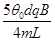
【解析】(1)粒子运动的半径为
R=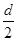 ①
①
由牛顿第二定律
qvB=m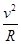 ②
②
匀速圆周运动的周期
T=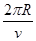 ③
③
粒子在磁场中运动的时间
t=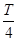 =
=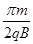 . ④
. ④
(2)如图所示,设粒子运动临界半径分别为R1和R2
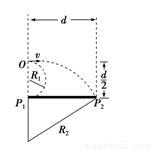
R1=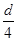 ⑤
⑤
d2+(R2-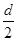 )2=R22
)2=R22
R2=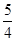 d ⑥
d ⑥
设粒子临界速度分别为v1和v2,
由②⑤⑥式,得
v1=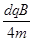 ⑦
⑦
v2=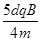 ⑧
⑧
若粒子通过两转盘,由题设可知
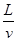 =
=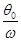 ⑨
⑨
联立⑦⑧⑨,得对应转盘的转速分别为
ω1=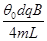
ω2=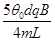
粒子要打在感光板上,需满足条件
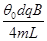 ≤ω≤
≤ω≤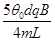 .
.

 ,粒子电荷量为q,质量为m,不计重力.
,粒子电荷量为q,质量为m,不计重力.