题目内容
有一空间探测器围绕一球状行星作圆周运动.已知该行星的半径r=1750km,探测器在靠近行星表面附近运行的周期为T=2h.(1)估算该行星表面附近的重力加速度的值.(结果保留两位有效数字)
(2)经探测发现,该行星表面无生命存在,在其表面上.却覆盖着一层厚厚的冻结的二氧化碳(干冰).有人建议用化学方法把二氧化碳分解为碳和氧气而在行星上面产生大气.由予行星对大气吸引力的作用,行星的表面将形成一定的大气压强.如果每1s分解可得106kg氧气,要使行星表面附近得到的大气压强为p=0.2atm,试估算至少需要多少时间才能完成?(已知球面积的计算公式S=4πr2,球体积的计算公式
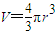 ;大气层的厚度与行星的半径相比很小;行星表面的温度较低,在此种情况下,二氧化碳的蒸发可以忽略不计;结果保留两位有效数字)
;大气层的厚度与行星的半径相比很小;行星表面的温度较低,在此种情况下,二氧化碳的蒸发可以忽略不计;结果保留两位有效数字)
【答案】分析:(1)空间探测器围绕一球状行星作圆周运动,根据重力提供向心力列式求解;
(2)根据P=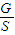 求解大气的质量.
求解大气的质量.
解答:解:(1)设探测器的质量为m,行星表面的重力加速度为g,有:
mg=m(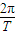 )2r
)2r
即g=(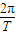 )2r
)2r
代入数据得:g≈1.3m/s2;
(2)该行星表面大气(氧气)的压力F可以近似表示为:
F=PS
其中 F=mg
S=4πr2
则大气(氧气)的质量m可以近似表示为:m=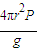
代入数据得:m=5.9×1017kg
由于1s分解可得106kg的氧气,则需要的时间为:t=5.9×1011s≈1.9×104年;
答:(1)该行星表面附近的重力加速度的值约为1.3m/s2.
(2)至少需要1.9×104年的时间才能完成.
点评:本题关键根据重力提供向心力列式求解重力加速度,第二问根据P=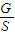 求解大气的重力G,较难.
求解大气的重力G,较难.
(2)根据P=
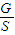 求解大气的质量.
求解大气的质量.解答:解:(1)设探测器的质量为m,行星表面的重力加速度为g,有:
mg=m(
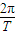 )2r
)2r即g=(
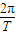 )2r
)2r代入数据得:g≈1.3m/s2;
(2)该行星表面大气(氧气)的压力F可以近似表示为:
F=PS
其中 F=mg
S=4πr2
则大气(氧气)的质量m可以近似表示为:m=
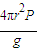
代入数据得:m=5.9×1017kg
由于1s分解可得106kg的氧气,则需要的时间为:t=5.9×1011s≈1.9×104年;
答:(1)该行星表面附近的重力加速度的值约为1.3m/s2.
(2)至少需要1.9×104年的时间才能完成.
点评:本题关键根据重力提供向心力列式求解重力加速度,第二问根据P=
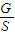 求解大气的重力G,较难.
求解大气的重力G,较难. 
练习册系列答案
相关题目