��Ŀ����
18���÷���������Ƴɵ�LED�ƾ��з���Ч�ʸߡ�ʹ�����������ŵ㣬�������������еõ��㷺Ӧ�ã���������ܾ��е����ԣ���������С���������ܴ�ijͬѧ����á����С���ݵķ����������ߡ��ķ������о���������ܵķ������ԣ���1��ʵ�����жϷ�������ܵ�����������ͼ1��ʾ����������ܵ��������߳��̲�һ�������׳�Ϊ��������ܵġ����š��͡��̽š�����ͬѧʹ�ö��õ��ŷķ���ġ���1k���������������ܵĵ��裬�����������ܡ��̽š��Ӵ����ڱ���������ܡ����š��Ӵ�����ָ�뼸�������������Ӵ��ź�ָ��ƫת�����ͼ2��ʾ��������ܵġ����š�Ϊ�����ܵĸ�����ѡ�������������������ͼ�ɶ�����ʱ�����ܵ���ֵΪ4000����
��2����ͬѧ�������ͼ3��ʾ�ĵ�·������������ܵ�����������ԣ�������ܵġ����š�Ӧ��ͼ���е�a��ѡ�a����b���������ӣ�
��3���밴ͼ3�ĵ�·ͼ��ͼ4�л������ߣ����������ӳ�ʵ���·��
��4����ͬѧ��÷�������ܵ������������������ͼ5��ʾ��ʵ��ʱ���֣�����ѹ��ʾ��U=0.8Vʱ����������ܿ�ʼ���⣮��ô�����ж���ͼ2״̬�·�������ܷ��⣨ѡ����⡱�����⡱����

���� ����ٵĹؼ�������ָ��û����̶��߶��룬���Թ���һλ����ڵĹؼ�����ȷ�ڱ�����ŷķ���ڲ���ص�����������������븺����������ܵĹؼ��ǻ�һ��б�ʵ���7.9��ͨ��ԭ�����бֱ�ߣ�Ȼ�������ͼ�߽���������꼴�ɣ�
��� 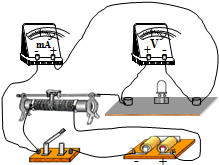 �⣺�ٺ����������ܡ��̽š��Ӵ����ڱ���������ܡ����š��Ӵ�����ָ�뼸��������˵�������ܲ���ͨ�����Զ����ܵġ����š�Ϊ�����ܵĸ�����
�⣺�ٺ����������ܡ��̽š��Ӵ����ڱ���������ܡ����š��Ӵ�����ָ�뼸��������˵�������ܲ���ͨ�����Զ����ܵġ����š�Ϊ�����ܵĸ�����
ŷķ���Ķ���Ϊ��R=4.0��1k=4000����
�ڸ�ͬѧ�������ͼ3��ʾ�ĵ�·������������ܵ�����������ԣ����ںڱ�����ŷķ���ڲ���ص��������������Է�������ܵġ����š�Ӧ��ͼ���е�a�����ӣ�
������ͼ��ͼ��ʾ��
�ܸ��ݢ��еķ�����֪��ͼ������¶����ܴ��ڵ�ͨ״̬������R=$\frac{U}{I}$��֪����I-Uͼ���У���һ����б��Ϊ4��ͨ��ԭ�����бֱ�ߣ�����ֱ��������������ߵĽ�������������0.8V�����������ܵķ����ѹ���ʶ����ܷ��⣮
�ʴ�Ϊ����1������ 4000����2��a����3����ͼ��ʾ����4������
���� Ӧ��ȷ����ŷķ���ڱ������ڲ���ص�����������������븺���������ڸ���R=$\frac{U}{I}$��֪��U-I�ϵĵ���ԭ�����ߵ�б�ʵ��ڵ��裮

 ��Ǭ����������ҵ���ּ����ӱ����������ϵ�д�
��Ǭ����������ҵ���ּ����ӱ����������ϵ�д�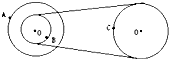 ��ͼ��ʾ��Ƥ������װ���У���A��Bͬ�ᣬA��B��C�ֱ��������ֱ�Ե���ʵ㣬��RA=RC=2RB��������˵������ȷ���ǣ�������
��ͼ��ʾ��Ƥ������װ���У���A��Bͬ�ᣬA��B��C�ֱ��������ֱ�Ե���ʵ㣬��RA=RC=2RB��������˵������ȷ���ǣ�������| A�� | ���ʵ�����ٶ�֮��vA��vB��vC=2��1��1 | |
| B�� | ���ʵ�Ľ��ٶ�֮�Ȧ�A����B����C=2��1��1 | |
| C�� | ���ʵ������֮��TA��TB��TC=2��2��1 | |
| D�� | ���ʵ��Ƶ��֮��fA��fB��fC=1��1��1 |
 ��ͼ��ʾ����x��0��y��0�Ŀռ��з���ֱ��xOyƽ���������ǿ�ų��������������������������ͬ�Ĵ������ӣ���x���ϵ�P���Բ�ͬ�ij��ٶ�ƽ����y������˴ų���Ȼ��ֱ��y���ϵ�M��N��������ų��������������������Ǽ������ã��Ƚ������ӵ��˶�������˵����ȷ���ǣ�������
��ͼ��ʾ����x��0��y��0�Ŀռ��з���ֱ��xOyƽ���������ǿ�ų��������������������������ͬ�Ĵ������ӣ���x���ϵ�P���Բ�ͬ�ij��ٶ�ƽ����y������˴ų���Ȼ��ֱ��y���ϵ�M��N��������ų��������������������Ǽ������ã��Ƚ������ӵ��˶�������˵����ȷ���ǣ�������| A�� | ��N����������ӳ��ٶȽϴ� | |
| B�� | ��N������������ڴų��еļ��ٶȽϴ� | |
| C�� | ��M������������ڴų��еĽ��ٶȽϴ� | |
| D�� | ��M������������ڴų��е�ʱ��϶� |
 ��ͼ��ʾ������Ϊm���������Ϊq �������ٶ�v ��ˮƽ�����45��ǽ�����ǿ�糡����ǿ�ų����ų�����ֱֽ����������������ֱ���˶���������˵����ȷ���ǣ�������
��ͼ��ʾ������Ϊm���������Ϊq �������ٶ�v ��ˮƽ�����45��ǽ�����ǿ�糡����ǿ�ų����ų�����ֱֽ����������������ֱ���˶���������˵����ȷ���ǣ�������| A�� | ���ܵ糡���������������������������� | |
| B�� | �������磬�����˶��е����ܲ������� | |
| C�� | ��ǿ�糡�ĵ糡ǿ��E=$\frac{2mg}{q}$ | |
| D�� | ��ǿ�ų��ĴŸ�Ӧǿ��B=$\frac{mg}{qv}$ |
 ��ͼ��ʾ���ڱڹ⻬���뾶ΪR�İ������������ڴֲڵ�ˮƽ���ϣ�OΪ���ģ���һ����ϵ��Ϊk���ᵯ��һ�˹̶��������ײ�A�㣬������һ��������Ϊm��С��������С��ֹ��B�㣮��֪OB��ˮƽ����ļн�Ϊ��=30�㣮����˵����ȷ���ǣ�������
��ͼ��ʾ���ڱڹ⻬���뾶ΪR�İ������������ڴֲڵ�ˮƽ���ϣ�OΪ���ģ���һ����ϵ��Ϊk���ᵯ��һ�˹̶��������ײ�A�㣬������һ��������Ϊm��С��������С��ֹ��B�㣮��֪OB��ˮƽ����ļн�Ϊ��=30�㣮����˵����ȷ���ǣ�������| A�� | ˮƽ������������ҵ�Ħ���� | B�� | �ᵯ�ɶ�С�����������СΪ$\frac{1}{2}$mg | ||
| C�� | ������С�����������СΪmg | D�� | ����ԭ��ΪR+$\frac{mg}{k}$ |
 ����ɾ��ȷֲ��ڰ������ϣ������ڴ˰��������O�������ĵ糡ǿ�ȴ�СΪE0���ֽ�һ��ͨ��O������������ɦ�=60���ƽ��Ѱ�����ֳ�һ��С��С�ꡱ���森��ͼ��ʾ�����ֳ��ġ�С�ꡱ�����ϵĵ����O�������糡�ĵ糡ǿ�ȴ�СΪ��������
����ɾ��ȷֲ��ڰ������ϣ������ڴ˰��������O�������ĵ糡ǿ�ȴ�СΪE0���ֽ�һ��ͨ��O������������ɦ�=60���ƽ��Ѱ�����ֳ�һ��С��С�ꡱ���森��ͼ��ʾ�����ֳ��ġ�С�ꡱ�����ϵĵ����O�������糡�ĵ糡ǿ�ȴ�СΪ��������| A�� | $\frac{1}{3}$E0 | B�� | $\frac{1}{2}$E0 | C�� | $\frac{{\sqrt{3}}}{2}$E0 | D�� | E0 |
| A�� | ��ʽF=G$\frac{{m}_{1}{m}_{2}}{{x}^{2}}$ֻ�����ڼ�������������֮����������� | |
| B�� | ���������ľ���r�ܽ�ʱ����������Ѳ����������������ʲ����ù�ʽF=G$\frac{{m}_{1}{m}_{2}}{{x}^{2}}$������ | |
| C�� | �������������ܵ�������������������ù�ʽF=G$\frac{{m}_{1}{m}_{2}}{{x}^{2}}$���� | |
| D�� | �ڽ����ڣ�ͬѧ֮��Ҳ���������� |
 ����������һ�����������IJ������䶥��ǡ��������Ӵ���Բ���ᣨͼ�����ߣ������洹ֱ�������ߵĽ���Ϊ�ȱ������Σ���ͼ��ʾ����һ�뾶Ϊr��Բ����ƽ�й�����ֱ���䵽Բ�������ϣ���������������Բ�����غϣ���֪������������Ϊn=$\sqrt{3}$��rΪ��֪����������е��ٶ�Ϊc����
����������һ�����������IJ������䶥��ǡ��������Ӵ���Բ���ᣨͼ�����ߣ������洹ֱ�������ߵĽ���Ϊ�ȱ������Σ���ͼ��ʾ����һ�뾶Ϊr��Բ����ƽ�й�����ֱ���䵽Բ�������ϣ���������������Բ�����غϣ���֪������������Ϊn=$\sqrt{3}$��rΪ��֪����������е��ٶ�Ϊc����