题目内容
(2010?海南)在水平的足够长的固定木板上,一小物块以某一初速度开始滑动,经一段时间t后停止.现将该木板改置成倾角为45°的斜面,让小物块以相同的初速度沿木板上滑.若小物块与木板之间的动摩擦因数为μ.则小物块上滑到最高位置所需时间与t之比为( )
分析:对物块在水平面和斜面上进行受力分析,运用牛顿第二定律结合运动学公式解决.
解答:解:木板水平时,物块的合力是滑动摩擦力.根据牛顿第二定律得出:
小物块的加速度a1=μg,
设滑行初速度为v0,则滑行时间为t=
;
木板改置成倾角为45°的斜面后,对物块进行受力分析:
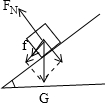
小滑块的合力F合=mgsin45°+f=mgsin45°+μmgcos45°
小物块上滑的加速度a2=
=
,
滑行时间t′=
=2
,
因此
=
=
,
故选A.
小物块的加速度a1=μg,
设滑行初速度为v0,则滑行时间为t=
| v0 |
| μg |
木板改置成倾角为45°的斜面后,对物块进行受力分析:

小滑块的合力F合=mgsin45°+f=mgsin45°+μmgcos45°
小物块上滑的加速度a2=
| mgsin45°+μmgcos45° |
| m |
(1+μ)
| ||
| 2 |
滑行时间t′=
| v0 |
| a2 |
| v0 | ||
(1+μ)
|
因此
| t′ |
| t |
| a1 |
| a2 |
| ||
| 1+μ |
故选A.
点评:对物块在水平面和斜面上进行受力分析,运用牛顿第二定律结合运动学公式解决.注意情景发生改变,要重新进行受力分析.

练习册系列答案
相关题目
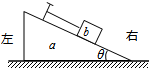 (2010?海南)如图,水平地面上有一楔形物块a,其斜面上有一小物块b,b与平行于斜面的细绳的一端相连,细绳的另一端固定在斜面上.a与b之间光滑,a和b以共同速度在地面轨道的光滑段向左运动.当它们刚运行至轨道的粗糙段时( )
(2010?海南)如图,水平地面上有一楔形物块a,其斜面上有一小物块b,b与平行于斜面的细绳的一端相连,细绳的另一端固定在斜面上.a与b之间光滑,a和b以共同速度在地面轨道的光滑段向左运动.当它们刚运行至轨道的粗糙段时( )
 (2010?海南模拟)一质量为0.5kg的滑块以6m/s的初速度冲上一倾角为30°足够长的斜面,某同学利用DIS实验系统测出了滑块冲上斜面过程中多个时刻的瞬时速度,如图所示为通过计算机绘制出的滑块上滑过程的v-t图.求:(g取10m/s.)
(2010?海南模拟)一质量为0.5kg的滑块以6m/s的初速度冲上一倾角为30°足够长的斜面,某同学利用DIS实验系统测出了滑块冲上斜面过程中多个时刻的瞬时速度,如图所示为通过计算机绘制出的滑块上滑过程的v-t图.求:(g取10m/s.) (2010?海南模拟)如图,质量为M的楔形物A静置在水平地面上,其斜面的倾角为θ,斜面上有一质量为m的小物块B,B与斜面之间存在摩擦.用恒力F沿斜面向上拉B,使之匀速上滑.在B运动的过程中,楔形物块A始终保持静止.关于相互间作用力的描述正确的有( )
(2010?海南模拟)如图,质量为M的楔形物A静置在水平地面上,其斜面的倾角为θ,斜面上有一质量为m的小物块B,B与斜面之间存在摩擦.用恒力F沿斜面向上拉B,使之匀速上滑.在B运动的过程中,楔形物块A始终保持静止.关于相互间作用力的描述正确的有( )