题目内容
16.某同学在“研究平抛物体的运动”实验中,已经判定平抛运动在竖直方向为为自由落体运动后,再来用下图甲所示实验装置研究水平方向的运动.他先调整斜槽轨道槽口末端水平,然后在方格纸(甲图中未画出方格)上建立好直角坐标系xOy,将方格纸上的坐标原点O与轨道槽口末端重合,Oy轴与重垂线重合,Ox轴水平.实验中使小球每次都从斜槽同一高度由静止滚下,经过一段水平轨道后抛出.依次均匀下移水平挡板的位置,分别得到小球在挡板上的落点,并在方格纸上标出相应的点迹,再用平滑曲线将方格纸上的点迹连成小球的运动轨迹如图7乙所示.已知方格边长为L,重力加速度为g.
(1)请你写出判断小球水平方向是匀速运动的方法(请在轨迹图上作图配合说明):在轨迹上取坐标为(3L,L)、(6L,4L)、(9L,9L)的三点,分别记为A、B、C点,其纵坐标y1:y2:y3=1:4:9,由于已研究得出小球在竖直方向是自由落体运动,因此可知从抛出到A点所用时间t1与从A点到B点所用时间t2、从B点到C点所用时间t3相等,这三点的横坐标之间的距离也相等,说明了在相等时间内水平位移相等,即说明平抛运动在水平方向的运动为匀速直线运动
(2)小球平抛的初速度v0=$\frac{3\sqrt{2gL}}{2}$
(3)小球竖直下落距离y与水平运动距离x的关系式为:y=$\frac{{x}^{2}}{9L}$
(4)为了能较准确的描绘运动轨迹,下面列出了一些操作要求,你认为正确的是A
A.通过调节使斜槽末端的切线保持水平
B.实验所用斜槽的轨道必须是光滑的
C.每次必须由静止释放小球而释放小球的位置可以不同
D.将球的位置标在纸上后,取下纸,用直尺将点连成折线.
分析 通过相等时间内水平方向上的位移是否相等来判断水平方向上运动是否是匀速直线运动,根据平抛运动在水平方向和竖直方向上的运动规律求出平抛运动的初速度以及竖直位移与水平位移的关系.
解答 解:(1)在轨迹上取坐标为(3L,L)、(6L,4L)、(9L,9L)的三点,分别记为A、B、C点,其纵坐标y1:y2:y3=1:4:9,由于已研究得出小球在竖直方向是自由落体运动,因此可知从抛出到A点所用时间t1与从A点到B点所用时间t2、从B点到C点所用时间t3相等,这三点的横坐标之间的距离也相等,说明了在相等时间内水平位移相等,即说明平抛运动在水平方向的运动为匀速直线运动.
(2)根据L=$\frac{1}{2}$gt2得:t=$\sqrt{\frac{2L}{g}}$,
解得:v0=$\frac{3L}{t}$=$\frac{3\sqrt{2gL}}{2}$.
(3)根据x=v0t,y=$\frac{1}{2}$gt2=$\frac{1}{2}$g($\frac{x}{{v}_{0}}$)2=$\frac{{x}^{2}}{9L}$.
(4)A、为了保证小球做平抛运动,斜槽的末端切线必须水平.故A正确.
B、实验时斜槽不一定需要光滑,只要小球每次从同一位置由静止释放即可.故B、C错误.
D、将球的位置标在纸上后,取下纸,用平滑曲线连接得到平抛运动的轨迹.故D错误.
故选:A.
故答案为:(1)在轨迹上取坐标为(3L,L)、(6L,4L)、(9L,9L)的三点,分别记为A、B、C点,其纵坐标y1:y2:y3=1:4:9,由于已研究得出小球在竖直方向是自由落体运动,因此可知从抛出到A点所用时间t1与从A点到B点所用时间t2、从B点到C点所用时间t3相等,这三点的横坐标之间的距离也相等,说明了在相等时间内水平位移相等,即说明平抛运动在水平方向的运动为匀速直线运动.
(2)$\frac{3\sqrt{2gL}}{2}$;(3)$\frac{{x}^{2}}{9L}$;(4)A.
点评 解决本题的关键知道平抛运动在水平方向上和竖直方向上的运动规律,结合运动学公式灵活求解.


| A. | t=0.01s时矩形金属线框平面与磁感线平行 | |
| B. | 该线圈1s转过100圈 | |
| C. | 该交变电动势的周期为2s | |
| D. | 电动势瞬时值为22V时,线圈平面与中性面的夹角为45° |
 利用霍尔效应制作的霍尔元件,广泛应用于测量和自动控制等领域.如图是霍尔元件的工作原理示意图,磁感应强度B垂直于霍尔元件的工作面向下,通入图示方向的电流I,M、N两侧面会形成电势差UMN,下列说法中正确的是( )
利用霍尔效应制作的霍尔元件,广泛应用于测量和自动控制等领域.如图是霍尔元件的工作原理示意图,磁感应强度B垂直于霍尔元件的工作面向下,通入图示方向的电流I,M、N两侧面会形成电势差UMN,下列说法中正确的是( )| A. | 霍尔元件能够把电学量转换为磁学量的传感器 | |
| B. | 若霍尔元件的载流子是自由电子,则电势差UMN<0 | |
| C. | 仅增大磁感应强度时,电势差UMN变大 | |
| D. | 在测定地球赤道上方的地磁场强弱时,元件的工作面应保持水平 |



 2011年4月,在伦敦举行的国际奥委会执委会上确认,女子跳台滑雪等6个新项目加入2014年冬奥会.如图所示,运动员踏着专用滑雪板,不带雪杖在助滑路上(末画出)获得一速度后水平飞出,在空中飞行一段距离后着陆,这项运动非常惊险.设一位运动员由斜坡顶的A点沿水平方向飞出的速度v0=20m/s,落点在斜坡L的B点,斜坡倾角θ取37°,斜坡可以看成一斜面.(取g=10m/s2,sin 37°=0.6,cos37°=0.8)求:
2011年4月,在伦敦举行的国际奥委会执委会上确认,女子跳台滑雪等6个新项目加入2014年冬奥会.如图所示,运动员踏着专用滑雪板,不带雪杖在助滑路上(末画出)获得一速度后水平飞出,在空中飞行一段距离后着陆,这项运动非常惊险.设一位运动员由斜坡顶的A点沿水平方向飞出的速度v0=20m/s,落点在斜坡L的B点,斜坡倾角θ取37°,斜坡可以看成一斜面.(取g=10m/s2,sin 37°=0.6,cos37°=0.8)求:
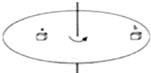 如图所示,质量之比为2:3的a、b两物体放在粗糙的圆盘上,a、b到圆心的距离之比是3:2,圆盘绕圆心做匀速圆周运动,两物体相对圆盘静止,a、b两物体做圆周运动的向心力之比是( )
如图所示,质量之比为2:3的a、b两物体放在粗糙的圆盘上,a、b到圆心的距离之比是3:2,圆盘绕圆心做匀速圆周运动,两物体相对圆盘静止,a、b两物体做圆周运动的向心力之比是( ) 如图所示,两根足够长的光滑金属导轨MN、PQ间距为l=0.5m,其电阻不计,两导轨及其构成的平面均与水平面成30°角.完全相同的两金属棒ab、cd分别垂直导轨放置,每棒两端都与导轨始终有良好接触,已知两棒的质量均为0.02kg,电阻均为R=0.1Ω,整个装置处在垂直于导轨平面向上的匀强磁场中,磁感应强度为B=0.2T,棒ab在平行于导轨向上的力F作用下,沿导轨向上匀速运动,而棒cd恰好能保持静止.取g=10m/s2,问:
如图所示,两根足够长的光滑金属导轨MN、PQ间距为l=0.5m,其电阻不计,两导轨及其构成的平面均与水平面成30°角.完全相同的两金属棒ab、cd分别垂直导轨放置,每棒两端都与导轨始终有良好接触,已知两棒的质量均为0.02kg,电阻均为R=0.1Ω,整个装置处在垂直于导轨平面向上的匀强磁场中,磁感应强度为B=0.2T,棒ab在平行于导轨向上的力F作用下,沿导轨向上匀速运动,而棒cd恰好能保持静止.取g=10m/s2,问: