��Ŀ����
����Ŀ��һ���������ȱ���ֱ���˶������ٶ�Ϊv0�����ٶ�Ϊa���˶�ʱ��Ϊt��ĩ�ٶ�Ϊv��λ��Ϊx��������������⡣
(1)���ݼ��ٶȵĶ���ʽ���Ƶ��ȱ���ֱ���˶���v-t��ϵ��v=v0+at
(2)�����ȱ���ֱ���˶���v-t��ϵ�Լ�x-t��ϵ���Ƶ��ȱ����˶��ٶ�-λ�ƹ�ϵʽ��v2-v02=2ax
(3)������һ��ʱ���ڵ�ƽ���ٶ�![]() ����Ϊ��
������![]() =
=![]() �����У�tΪ�˶�����ʱ�䣬xΪ���ʱ���ڵ���λ�ơ���v1��ʾ�ȱ���ֱ���˶��е�ʱ�̣���
�����У�tΪ�˶�����ʱ�䣬xΪ���ʱ���ڵ���λ�ơ���v1��ʾ�ȱ���ֱ���˶��е�ʱ�̣���![]() ����˲ʱ�ٶȡ���֤�����������ȱ���ֱ���˶�ʱ��v1=
����˲ʱ�ٶȡ���֤�����������ȱ���ֱ���˶�ʱ��v1=![]() =
=![]()
���𰸡���1����������2����������3��������
��������
(1)�ɼ��ٶȶ���ʽa=![]() ���ٶȱ仯��
���ٶȱ仯��![]() =v-v0��
=v-v0��![]() =t
=t
��
a=![]()
������
v=v0+at
(2)���ٶȹ�ʽv=v0+at��λ�ƹ�ʽx=v0t+![]() at2
at2
��ʽ��ȥʱ��������
v2-v02=2ax
(3)���ٶȹ�ʽ![]()
![]() =
=![]() =
=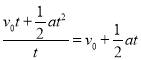
����![]() =v1����Ϊv=v0+at��
=v1����Ϊv=v0+at��
����v1-v0=![]() at��
at��
v-v1=![]() at
at
����
2v1=v+v0
������
v1=![]() =
=![]()

��ϰ��ϵ�д�
�����Ŀ