Question

【题目】如图所示，距地面高度h=5 m的平台边缘水平放置一两轮间距为d=6 m的传送带，一可视为质点的物块从光滑平台边缘以v0=5 m/s的初速度滑上传送带，已知物块与传送带间的动摩擦因数μ=0.2。取重力加速度大小g=10 m/s2。求：

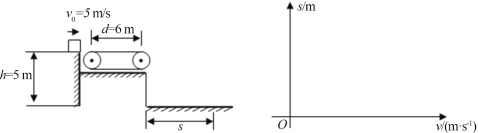
（1）若传送带不动，小物块离开传送带右边缘落地的水平距离；

（2）试分析传送带的速度满足什么条件时，小物块离开传送带右边缘落地的水平距离最大，并求最大距离；

（3）设传送带的速度为v′且规定传送带顺时针运动时v′为正，逆时针运动是v′为负。试分析在图中画出小物块离开传送带右边缘落地的水平距离s与v′的变化关系图线（不需要计算过程，只需画出图线即可）。

Answer 1

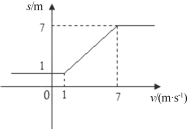
【答案】（1）x1=1 m （2）x2=7 m （3）见解析图

【解析】（1）若传送带静止，物块一直匀减速，根据动能定理，有：

解得：v1=1 m/s

平抛运动的时间：

故射程为：x1=v1t=1×1=1 m

（2）如果小物块在传送带上一直加速，则离开传送带的速度最大，根据动能定理，有：

解得：v2=7 m/s

故射程为：x2=v2t=7×1=7 m

（3）如果传送带顺时针转动，速度v′≥7 m/s，物体一直加速，射程最远，为7 m；

如果传送带顺时针转动，速度1 m/s≤v′<7 m/s，物体先加速后匀速，射程：x=v′t=v′；

如果传送带顺时针转动，速度v′<1 m/s，物体一直减速，射程为1 m；

如果传送带逆时针转动，物体一直减速，射程为1 m；

故s–v′图象如图所示：