题目内容
经过天文望远镜长期观测,人们在宇宙中已发现了许多双星系统.双星系统由两个星体构成,其中每个星体的线度都远小于两星体之间的距离.一般双星系统距离其他星体很远,可以当做孤立系统处理.现根据对某一双星系统的观测量确定,该双星系统中每个星体的质量都是M,两者相距l,它们正围绕两者连线的中点做圆周运动.(1)试计算该双星系统的运动周期 .(2)若实验上观察测得的运动周期为
.(2)若实验上观察测得的运动周期为 ,且
,且 .为了解释二者的不同,目前有一种流行的理论认为在宇宙中可能有一种望远镜观测不到的物质,即暗物质.作为一种简化模型,我们假定在以这两个星体连线为直径的球体内均匀分布着这种暗物质,而不考虑其他暗物质的影响.试根据这一模型和上述观测结果确定该星系间这种暗物质的密度.
.为了解释二者的不同,目前有一种流行的理论认为在宇宙中可能有一种望远镜观测不到的物质,即暗物质.作为一种简化模型,我们假定在以这两个星体连线为直径的球体内均匀分布着这种暗物质,而不考虑其他暗物质的影响.试根据这一模型和上述观测结果确定该星系间这种暗物质的密度.
答案:略
解析:
解析:
|
解: (1)双星均绕它们的连线中点做圆周运动,设运动速率为v,由万有引力提供向心力有 , ,
(注:万有引力 解得 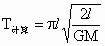
(2)由题可知观测到星体的运动周期为
说明双星系统中受到的向心力大于本身的万有引力,故它还受其他指向中心的作用力.按照题意这一作用来源于均匀分布的暗物质. (根据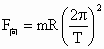 知,m、R一定时, 知,m、R一定时, 较小.说明双星的向心力比计算出的引力要大) 较小.说明双星的向心力比计算出的引力要大)
设均匀分布的暗物质 (直径为l的球形)质量为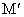 ,则双星做圆周运动的向心力由双星间万有引力与暗物质对双星的引力的合力提供,有 ,则双星做圆周运动的向心力由双星间万有引力与暗物质对双星的引力的合力提供,有
由题意 
又 
由①②③解得 
暗物质的体积为  , ,
所以暗物质的密度 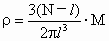
本题以天文学的前沿科技知识为载体,介绍了双星系统和暗物质,考查了分析推理、空间想像能力;同时又开阔了科技视野.这类题型在高考中经常出现. |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,r=l,向心力
,r=l,向心力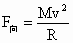 中,
中, )
)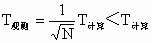 .(N>1,
.(N>1, )
)
 .(2)若实验上观察测得的运动周期为
.(2)若实验上观察测得的运动周期为 ,且
,且 .为了解释二者的不同,目前有一种流行的理论认为在宇宙中可能有一种望远镜观测不到的物质,即暗物质.作为一种简化模型,我们假定在以这两个星体连线为直径的球体内均匀分布着这种暗物质,而不考虑其他暗物质的影响.试根据这一模型和上述观测结果确定该星系间这种暗物质的密度.
.为了解释二者的不同,目前有一种流行的理论认为在宇宙中可能有一种望远镜观测不到的物质,即暗物质.作为一种简化模型,我们假定在以这两个星体连线为直径的球体内均匀分布着这种暗物质,而不考虑其他暗物质的影响.试根据这一模型和上述观测结果确定该星系间这种暗物质的密度.