Question

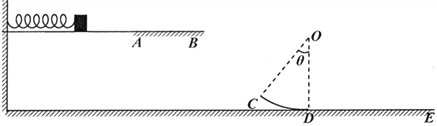
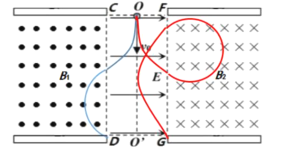
【题目】如图所示，有一束等离子体（设粒子质量均为m，电荷量分别为+q和－q）以相同速度大小由O点沿OO′直线入射等离体分离装置，速度大小为v0=2×105m/s。在平行板间存在着磁感应强度分别为B1（垂直纸面向外）、B2（垂直纸面向里）的匀强磁场。其中CD、FG为磁场的边界，且CD、FG之间存在水平向右的匀强电场。已知电场强度大小E=4×104N/C，板间距为d=5cm，OO′为该区域的对称轴，CD与FG的距离为L=2cm。(设粒子的重力和相互之间的作用力均不计，且比荷均为=5×107C/kg。

(1)求带正电的粒子在进入磁场时速度方向与竖直线的夹角；

(2)若要使带负电的粒子进出磁场一次后，由下方DG之间离开电场，求磁感应强度B1的取值范围；

(3)若左右两区域的磁感应强度大小B1=B2=B，要使两种粒子进出磁场一次后，都由下方DG之间离开电场，求磁感应强度B的取值范围。

Answer 1

【答案】(1)；(2)；(3)

【解析】

(1)根据动能定理可得

可得

故与竖直线夹角

(2)负粒子，恰到D点临界，半径应小于此临界值，对应的磁感应强度设为B1，可得弦长为

=(5－2)cm=3cm

根据洛伦兹力提供向记力，则有

可得

故

(3)正粒子，恰到G点临界，半径应小于此临界值，对应的磁感应强度设为B2，可得弦长为

r2=(4－3)cm=1cm

轨迹半径

此时

cm

故不会撞到右上板，由，得

将r2代入得

B2=0.8T＞B1

综合分析得：磁感应强度只要大于B2，正粒子既不会再次进入磁场也不会打到板上，负粒子也不会打到板上，即