题目内容
17.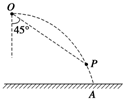 如图所示,某物体自空间O点以水平初速度v0抛出,落在地面上的A点,其轨迹为一抛物线.现仿此抛物线制作一个光滑滑道并固定在与OA完全重合的位置上,然后将此物体从O点由静止释放,受微小扰动而沿此滑道滑下,在下滑过程中物体未脱离滑道.P为滑道上一点,OP连线与竖直方向成45°角,则此物体( )
如图所示,某物体自空间O点以水平初速度v0抛出,落在地面上的A点,其轨迹为一抛物线.现仿此抛物线制作一个光滑滑道并固定在与OA完全重合的位置上,然后将此物体从O点由静止释放,受微小扰动而沿此滑道滑下,在下滑过程中物体未脱离滑道.P为滑道上一点,OP连线与竖直方向成45°角,则此物体( )| A. | 由O运动到P点的时间大于$\frac{2{v}_{0}}{g}$ | |
| B. | 物体经过P点时,速度的水平分量为$\frac{2\sqrt{5}}{5}$v0 | |
| C. | 物体经过P点时,速度的竖直分量为2v0 | |
| D. | 物体经过P点时的速度大小为$\sqrt{5}$v0 |
分析 若做平抛运动,OP连线与竖直方向成45°角,所以竖直分位移与水平分位移大小相等,根据时间可求出竖直方向的分速度和速度的大小和方向,若从O点由静止释放,受微小扰动而沿此滑道滑下,运动过程中只有重力做功,速度方向沿切线方向.
解答 解:A、物体若做平抛运动,有:${v}_{0}t=\frac{1}{2}g{t}^{2}$,则t=$\frac{2{v}_{0}}{g}$.而物体的运动除受重力外,还受到支持力作用,加速度小于重力加速度,则时间大于$\frac{2{v}_{0}}{g}$.故A正确.
B、物体若做平抛运动,运动到P点时竖直方向上的分速度:vy=gt=2v0,此时速度与水平方向的夹角为α,则有:$sinα=\frac{{v}_{y}}{\sqrt{{{v}_{y}}^{2}+{{v}_{0}}^{2}}}$=$\frac{2\sqrt{5}}{5}$.物块沿该轨道滑动,只有重力做功,根据动能定理得,mgh=$\frac{1}{2}m{v}^{2}$,解得:${v}^{2}=2gh={{v}_{y}}^{2}$,所以v=2v0.则物体经过P点时,速度的竖直分量:${v}_{y}′=2{v}_{0}sinα=\frac{4\sqrt{5}}{5}{v}_{0}$.速度的水平分量${v}_{x}′=2{v}_{0}cosα=\frac{2\sqrt{5}}{5}{v}_{0}$.故B正确,CD错误.
故选:AB
点评 解决本题的关键掌握处理平抛运动的方法,注意物体的运动情况与平抛运动的情况不同,难度适中.

练习册系列答案
相关题目
7.做匀变速直线运动的物体,它在第1s内通过的位移14m,在第3s内通过的位移6m,那么该运动物体的( )
| A. | 加速度为-8m/s2,初速度为14m/s | B. | 加速度为-4m/s2,初速度为16m/s | ||
| C. | 经过3.5s后物体的速度变为0 | D. | 经过4s后物体的速度变为0 |
8.自行车在平直公路上匀速行驶,前后车轮所受地面摩擦力方向为( )
| A. | 前后车轮所受摩擦力都向后 | |
| B. | 前后车轮所受摩擦力都向前 | |
| C. | 前车轮所受摩擦力向后,后车轮所受摩擦力向前 | |
| D. | 前车轮所受摩擦力向前,后车轮所受摩擦力向后 |
12. 如图所示,把一个带电小球A固定在光滑绝缘水平桌面上,桌面足够大,在桌面的另一处放置一带电小球B,现给小球B一个垂直AB连线的初速度v0,使其在桌面上运动,则下列说法不正确的是( )
如图所示,把一个带电小球A固定在光滑绝缘水平桌面上,桌面足够大,在桌面的另一处放置一带电小球B,现给小球B一个垂直AB连线的初速度v0,使其在桌面上运动,则下列说法不正确的是( )
 如图所示,把一个带电小球A固定在光滑绝缘水平桌面上,桌面足够大,在桌面的另一处放置一带电小球B,现给小球B一个垂直AB连线的初速度v0,使其在桌面上运动,则下列说法不正确的是( )
如图所示,把一个带电小球A固定在光滑绝缘水平桌面上,桌面足够大,在桌面的另一处放置一带电小球B,现给小球B一个垂直AB连线的初速度v0,使其在桌面上运动,则下列说法不正确的是( )| A. | 若A、B为同种电荷,B球一定做速度变大的曲线运动 | |
| B. | 若A、B为同种电荷,B球一定做加速度变大的曲线运动 | |
| C. | 若A、B为异种电荷,B球可能做速度、加速度都变小的曲线运动 | |
| D. | 若A、B为异种电荷,B球可能做速度大小和加速度大小都不变的曲线运动 |
2.如图(a),一物块在t=0时刻滑上一固定斜面,其运动的v-t图线如图(b)所示,若重力加速度及图中的v0、v1、t1均为已知量,且有sin2θ+cos2θ=1则可求出( )

| A. | 物块的质量 | B. | 物块与斜面间的动摩擦因数 | ||
| C. | 物块沿斜面上滑的最大距离 | D. | 物块滑回斜面底端时的速度 |
9.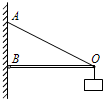 城市中的路灯、无轨电车的供电线路等,经常用三角形的结构悬挂.图是这类结构的一种简化模型,硬杆左端可绕通过B点且垂直于纸面的轴无摩擦的转动,右端O点通过钢索挂于A点,钢索和硬杆所受的重力均可忽略.有一质量不变的重物悬挂于O点,现将钢索缓慢变短,并使钢索的悬挂点A缓慢向下移动,以保证硬杆始终处于水平.则在上述变化过程中,下列说法中正确的是( )
城市中的路灯、无轨电车的供电线路等,经常用三角形的结构悬挂.图是这类结构的一种简化模型,硬杆左端可绕通过B点且垂直于纸面的轴无摩擦的转动,右端O点通过钢索挂于A点,钢索和硬杆所受的重力均可忽略.有一质量不变的重物悬挂于O点,现将钢索缓慢变短,并使钢索的悬挂点A缓慢向下移动,以保证硬杆始终处于水平.则在上述变化过程中,下列说法中正确的是( )
 城市中的路灯、无轨电车的供电线路等,经常用三角形的结构悬挂.图是这类结构的一种简化模型,硬杆左端可绕通过B点且垂直于纸面的轴无摩擦的转动,右端O点通过钢索挂于A点,钢索和硬杆所受的重力均可忽略.有一质量不变的重物悬挂于O点,现将钢索缓慢变短,并使钢索的悬挂点A缓慢向下移动,以保证硬杆始终处于水平.则在上述变化过程中,下列说法中正确的是( )
城市中的路灯、无轨电车的供电线路等,经常用三角形的结构悬挂.图是这类结构的一种简化模型,硬杆左端可绕通过B点且垂直于纸面的轴无摩擦的转动,右端O点通过钢索挂于A点,钢索和硬杆所受的重力均可忽略.有一质量不变的重物悬挂于O点,现将钢索缓慢变短,并使钢索的悬挂点A缓慢向下移动,以保证硬杆始终处于水平.则在上述变化过程中,下列说法中正确的是( )| A. | 硬杆对O点的弹力不变 | |
| B. | 钢索对O点的拉力变小 | |
| C. | 钢索和硬杆对O点的作用力的合力变大 | |
| D. | 钢索和硬杆对O点的作用力的合力不变 |
6.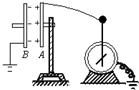 如图所示,用静电计可以测量已充电的平行板电容器两极之间的电势差,现使A板带正电,B板带负电,则下列说法正确的是( )
如图所示,用静电计可以测量已充电的平行板电容器两极之间的电势差,现使A板带正电,B板带负电,则下列说法正确的是( )
 如图所示,用静电计可以测量已充电的平行板电容器两极之间的电势差,现使A板带正电,B板带负电,则下列说法正确的是( )
如图所示,用静电计可以测量已充电的平行板电容器两极之间的电势差,现使A板带正电,B板带负电,则下列说法正确的是( )| A. | 将B板稍微向右移,静电计指针张角将变小 | |
| B. | 若将B板稍微向上移,静电计指针张角将变小 | |
| C. | 若将B板拿走,静电计指针张角变为零 | |
| D. | 若将玻璃板插入两极板之间,静电计指针张角将变小 |
 如图所示,电源向外电路提供恒压U=15V,已知:R1=6Ω,R2=9Ω,C=40μF.求
如图所示,电源向外电路提供恒压U=15V,已知:R1=6Ω,R2=9Ω,C=40μF.求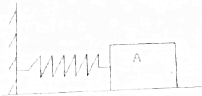 水平桌面上木块质量为15千克,与桌面之间的最大静摩擦力为为60牛.弹簧的劲度系数k=5000牛/米,如图所示,在木块A上施加向左的水平推力,当弹簧被外力压缩1厘米时,撤去外力后,物体将处于静止状态,此时木块受到的摩擦力为50牛,当压缩量大于1.2厘米时,撤去外力后,木块将不能保持静止状态.
水平桌面上木块质量为15千克,与桌面之间的最大静摩擦力为为60牛.弹簧的劲度系数k=5000牛/米,如图所示,在木块A上施加向左的水平推力,当弹簧被外力压缩1厘米时,撤去外力后,物体将处于静止状态,此时木块受到的摩擦力为50牛,当压缩量大于1.2厘米时,撤去外力后,木块将不能保持静止状态.