题目内容
19.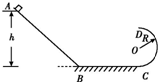 如图所示是在竖直平面内,由斜面和圆形轨道分别与水平面相切连接而成的光滑轨道,圆形轨道的半径为R,质量为m的小物块从斜面上距水平面高为h=2.5R的A点由静止开始下滑,物块通过轨道连接处的B、C点时,无机械能损失.求:
如图所示是在竖直平面内,由斜面和圆形轨道分别与水平面相切连接而成的光滑轨道,圆形轨道的半径为R,质量为m的小物块从斜面上距水平面高为h=2.5R的A点由静止开始下滑,物块通过轨道连接处的B、C点时,无机械能损失.求:(1)小物块通过B点时速度vB的大小;
(2)小物块能否通过圆形轨道的最高点D,若能,求出小物块过D点时的速度.
分析 (1)小物块从A点运动到B点的过程中,据机械能守恒定律求解.
(2)据机械能守恒求出最高点的速度,再与最高点的临界速度相比较即可判断.
解答 解:(1)小物块从A点运动到B点的过程中,由机械能守恒得:
mgh=$\frac{1}{2}m{{v}_{B}}^{2}$
解得:vB=$\sqrt{5gR}$.
(2)若小物块能从C点运动到D点,由动能定理得:
-mg•2R=$\frac{1}{2}m{{v}_{D}}^{2}-\frac{1}{2}m{{v}_{C}}^{2}$
解得:vD=$\sqrt{gR}$
设小物块通过圆形轨道的最高点的最小速度为vD1,
mg=m$\frac{{{v}_{D}}^{2}}{R}$
解得:vD1=$\sqrt{gR}$=vD
可知小物块恰能通过圆形轨道的最高点.
答:(1)小物块通过B点时速度vB的大小为$\sqrt{5gR}$;
(2)小物块恰能通过圆形轨道的最高点D,到达D点的速度大小为$\sqrt{gR}$.
点评 此题是动力学问题,解题思路清晰,利用动能定理或机械能守恒定律即可求解;注意圆周运动模型的综合应用,灵活应用临界条件判断是否通过最高点.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
7.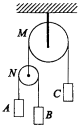 如图所示,M为定滑轮,一根细绳跨过M,一端系着物体C,另一端系着一动滑轮N,动滑轮N两侧分别悬挂着A、B两物体,已知B物体的质量为3kg,不计滑轮和绳的质量以及一切摩擦,若C物体的质量为9kg,则关于C物体的状态下列说法正确的是( )
如图所示,M为定滑轮,一根细绳跨过M,一端系着物体C,另一端系着一动滑轮N,动滑轮N两侧分别悬挂着A、B两物体,已知B物体的质量为3kg,不计滑轮和绳的质量以及一切摩擦,若C物体的质量为9kg,则关于C物体的状态下列说法正确的是( )
 如图所示,M为定滑轮,一根细绳跨过M,一端系着物体C,另一端系着一动滑轮N,动滑轮N两侧分别悬挂着A、B两物体,已知B物体的质量为3kg,不计滑轮和绳的质量以及一切摩擦,若C物体的质量为9kg,则关于C物体的状态下列说法正确的是( )
如图所示,M为定滑轮,一根细绳跨过M,一端系着物体C,另一端系着一动滑轮N,动滑轮N两侧分别悬挂着A、B两物体,已知B物体的质量为3kg,不计滑轮和绳的质量以及一切摩擦,若C物体的质量为9kg,则关于C物体的状态下列说法正确的是( )| A. | 当A的质量取值合适,C物体有可能处于平衡状态 | |
| B. | 无论A物体的质量是多大,C物体不可能平衡 | |
| C. | 当A的质量足够大时,C物体不可能向上加速运动 | |
| D. | 当A的质量取值合适,C物体可以向上加速也可以向下加速运动 |
14.两个带电量都是q的点电荷相距d时,它们之间的相互作用力为F.若使它们所带电量都减半、而距离加倍时,则它们之间的相互作用力为( )
| A. | F | B. | $\frac{F}{8}$ | C. | $\frac{F}{16}$ | D. | $\frac{F}{32}$ |
9.下列各组物理量均为矢量的是( )
| A. | 位移、时间、速度 | B. | 力、时间、路程 | ||
| C. | 力、平均速度、加速度 | D. | 质量、瞬时速度、加速度 |
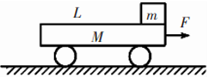 如图所示,平板小车静止于水平地面上,在其最右端放一可视为质点的小木块,已知木块的质量m=1kg,小车的质量M=4kg,上表面与木块间滑动摩擦因数μ=0.3,地面给小车的阻力与地面所受正压力成正比,比值为λ=0.2,现用向右的水平恒力F=30N拉平板小车,该水平恒力F作用的时间t1=2s,g取10m/s2.
如图所示,平板小车静止于水平地面上,在其最右端放一可视为质点的小木块,已知木块的质量m=1kg,小车的质量M=4kg,上表面与木块间滑动摩擦因数μ=0.3,地面给小车的阻力与地面所受正压力成正比,比值为λ=0.2,现用向右的水平恒力F=30N拉平板小车,该水平恒力F作用的时间t1=2s,g取10m/s2.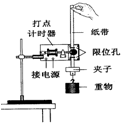 如图所示为用打点计时器验证机械能守恒定律的实验装置.
如图所示为用打点计时器验证机械能守恒定律的实验装置.