��Ŀ����
13��ij����̽�������������������������´���̽������DZ����Լ��ٶ�a�ȼ�����ֱ���գ������ٶȴﵽvʱ��������ͻȻ�������϶��رգ���֪�����ǵİ뾶ΪR���������DZ��渽����������������ٶ�Ϊg��̽�����������ı仯�����Ƕ�̽������������߶ȵı仯��������ת��Ӱ�졢���DZ���������̽������Ӱ�춼���Բ��ƣ�����1�����Ÿ����DZ�����Բ������е����ǵ��ٶȴ�С��
��2��̽�������������߶ȣ�
���� ��1���������������ṩ����������������������������������������DZ�����Բ���˶����ٶȣ�
��2�������ٶ�λ�ƹ�ʽ����ȼ���������λ�ƣ�����ٶ�λ�ƹ�ʽ����ȼ����˶���λ�ƣ��Ӷ��ó����������߶ȣ�
��� �⣺��1�������ǵ�����ΪM�����ǵ�����Ϊm�����ǵ��ٶ�Ϊv������ţ�ٵڶ�����
G$\frac{Mm}{R^2}=m\frac{v^2}{R}$
�����DZ����������������������$G\frac{Mm}{R^2}=mg$
������ã�v=$\sqrt{Rg}$
��2����̽��������������ʱ�����ĸ߶�Ϊh1���رշ������������ĸ߶�Ϊh2���������ܸ߶�Ϊh�������˶�ѧ��ʽ
v2=2ah1��v2=2gh2
��ã�$h={h_1}+{h_2}=\frac{v^2}{2}��\frac{1}{a}+\frac{1}{g}��$��
�𣺣�1�����Ÿ����DZ�����Բ������е����ǵ��ٶȴ�СΪ$\sqrt{Rg}$��
��2��̽�������������߶�Ϊ$\frac{{v}^{2}}{2}��\frac{1}{a}+\frac{1}{g}��$��
���� �������Ĺؼ����������������ɵ�������Ҫ���ۣ��Լ�֪��̽���������������е��˶����ɣ�����˶�ѧ��ʽ�����⣮

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
3�� ��ͼ��ʾ����Դ�綯��E=3.2V������R=30����С����L�Ķ��ѹUL=3.0V�������PL=4.5W��������S��1ʱ����ѹ���Ķ���Ϊ3V������S��2ʱ�����ݷ��������ǣ�������
��ͼ��ʾ����Դ�綯��E=3.2V������R=30����С����L�Ķ��ѹUL=3.0V�������PL=4.5W��������S��1ʱ����ѹ���Ķ���Ϊ3V������S��2ʱ�����ݷ��������ǣ�������
 ��ͼ��ʾ����Դ�綯��E=3.2V������R=30����С����L�Ķ��ѹUL=3.0V�������PL=4.5W��������S��1ʱ����ѹ���Ķ���Ϊ3V������S��2ʱ�����ݷ��������ǣ�������
��ͼ��ʾ����Դ�綯��E=3.2V������R=30����С����L�Ķ��ѹUL=3.0V�������PL=4.5W��������S��1ʱ����ѹ���Ķ���Ϊ3V������S��2ʱ�����ݷ��������ǣ�������| A�� | �ܰ����������� | B�� | �������� | C�� | �������������� | D�� | �п��ܱ��ջ� |
4��һ������ֱ���˶���ͼ����ͼ��ʾ��������壨������


| A�� | �����ȼ����˶��������ȼ����˶����ٶȷ�����ͬ | |
| B�� | �����ȼ����˶��������ȼ����˶����ٶȷ����෴ | |
| C�� | �����ȼ����˶��������ȼ����˶����ٶȷ�����ͬ | |
| D�� | �����ȼ����˶��������ȼ����˶����ٶȷ����෴ |
1�����������ʵ�ͬʱͬ����ͬһ������ֱ���˶������ǵ�v-tͼ����ͼ��ʾ���������жϴ�����ǣ�������


| A�� | 2sĩ���ϼ� | |
| B�� | t=2sʱ���������Զ | |
| C�� | ǰ4s�ڣ���ƽ���ٶȵ����ҵ�ƽ���ٶ� | |
| D�� | ���ϼ�ʱ�������40mԶ |
8��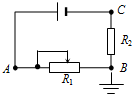 ��ͼ��ʾ����Դ�綯�Ʋ��䣬�ڵ��費�䣬��·��B��ӵأ��������������Ļ�Ƭ���һ���ʱ��A��C����ĵ��Ƶı仯�ǣ�������
��ͼ��ʾ����Դ�綯�Ʋ��䣬�ڵ��費�䣬��·��B��ӵأ��������������Ļ�Ƭ���һ���ʱ��A��C����ĵ��Ƶı仯�ǣ�������
 ��ͼ��ʾ����Դ�綯�Ʋ��䣬�ڵ��費�䣬��·��B��ӵأ��������������Ļ�Ƭ���һ���ʱ��A��C����ĵ��Ƶı仯�ǣ�������
��ͼ��ʾ����Դ�綯�Ʋ��䣬�ڵ��費�䣬��·��B��ӵأ��������������Ļ�Ƭ���һ���ʱ��A��C����ĵ��Ƶı仯�ǣ�������| A�� | ����ĵ��ƶ����� | B�� | ����ĵ��ƶ����� | ||
| C�� | A��ĵ������ߣ�C��ĵ��ƽ��� | D�� | A��ĵ��ƽ��ͣ�C��ĵ������� |
5��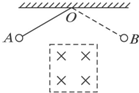 ��ͼ��ʾ����O�����·���һ����������߽�Ĵų����պϵ�ͭ����A���ɾ�ֹ�ͷ����Ұ�����ߵ�B�������ǿ���������������˵����ȷ���ǣ�������
��ͼ��ʾ����O�����·���һ����������߽�Ĵų����պϵ�ͭ����A���ɾ�ֹ�ͷ����Ұ�����ߵ�B�������ǿ���������������˵����ȷ���ǣ�������
 ��ͼ��ʾ����O�����·���һ����������߽�Ĵų����պϵ�ͭ����A���ɾ�ֹ�ͷ����Ұ�����ߵ�B�������ǿ���������������˵����ȷ���ǣ�������
��ͼ��ʾ����O�����·���һ����������߽�Ĵų����պϵ�ͭ����A���ɾ�ֹ�ͷ����Ұ�����ߵ�B�������ǿ���������������˵����ȷ���ǣ�������| A�� | ������Ϊ������� | B�� | ������Ϊ������� | ||
| C�� | A�����B�� | D�� | ͭ�������ȷ��ڶ� |
3����ˮ�������ʵ���У������ˮ���������Ƶ����5Hz��ˮ���Ĵ����ٶ�Ϊ0.05m/s��Ϊ�۲쵽��������������ijߴ����Ϊ��������
| A�� | 1cm | B�� | 10cm | C�� | 15cm | D�� | 20cm |
 ij����С����һ��̽����в���������ľ��֮��Ķ�Ħ��������ʵ��װ����ͼ��һ����ֲڵ�ľ��̶���ˮƽ�����ϣ�һ��װ�ж����֣�ľ������һ���飬��һ�����Ŵ���ʱ����ֽ����������һ��ͨ����������ֵ�ϸ�����������ӣ�����ʱ��ʹ�õĽ�����Դ��Ƶ��Ϊ50Hz����ʼʵ��ʱ���������з����������룬���鿪ʼ���ȼ����˶�����ֽ���ϴ��һϵ��С�㣮��ش��������⣺
ij����С����һ��̽����в���������ľ��֮��Ķ�Ħ��������ʵ��װ����ͼ��һ����ֲڵ�ľ��̶���ˮƽ�����ϣ�һ��װ�ж����֣�ľ������һ���飬��һ�����Ŵ���ʱ����ֽ����������һ��ͨ����������ֵ�ϸ�����������ӣ�����ʱ��ʹ�õĽ�����Դ��Ƶ��Ϊ50Hz����ʼʵ��ʱ���������з����������룬���鿪ʼ���ȼ����˶�����ֽ���ϴ��һϵ��С�㣮��ش��������⣺