��Ŀ����
11������ڿ�������ʱ���ܵ���������������f�Ĵ�С����εĽ����S�����ȣ��������������v�Ķ��η������ȣ���f=kSv2������kΪ��֪�ij������ܶ�Ϊ�ѡ��뾶Ϊr����Σ��Ӹ�Ϊh���Գ��ٶ�v0����С����ֱ���䣬���ǰ�Ѿ������˶�����֪�뾶Ϊr����������ΪV=$\frac{4}{3}$��r3���������ٶ�Ϊg������1��������ʱ���ٶ�vmax��
��2����������п�����������������Ĺ�W��
���� ��1��ץס������ܵ������Ϳ���������ȣ�������������ͺ�������ʽ�������ٶȵĴ�С��
��2��ȫ��������������������������ɶ��ܶ�������ÿ�������������
��� �⣺��1����ε�����m=$\frac{4}{3}��{r}^{3}��$
�����s=��r2
���������˶�ʱ����ks${v}_{max}^{2}$=mg
������ã�${v}_{max}=\sqrt{\frac{4��gr}{3k}}$
��2�����������̣��ɶ��ܶ�����mgh+W=$\frac{1}{2}m{v}_{max}^{2}-\frac{1}{2}m{v}_{0}^{2}$
��ã�W=$\frac{2}{3}�Ц�{r}^{3}��\frac{4��gr}{3k}-{v}_{0}^{2}-2gh��$
�𣺣�1��������ʱ���ٶ�Ϊ$\sqrt{\frac{4��gr}{3K}}$��
��2����������п�����������������Ĺ�Ϊ $\frac{2}{3}�Ц�{r}^{3}��\frac{4��gr}{3k}-{v}_{0}^{2}-2gh��$
���� ���⿼���˹�����ƽ���ţ�ٵڶ����ɵĻ������ã�֪������ٶ����ʱ��������������ȣ��ɶ��ܶ�����

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�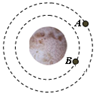 �칬һ���ɽϸߵIJ��Թ�����½����ϵ͵ĶԽӹ�������ɹ�������ʮ�Ž���Խӣ���ͼ��ʾ�����������ΪԲ���������˵������ȷ���ǣ�������
�칬һ���ɽϸߵIJ��Թ�����½����ϵ͵ĶԽӹ�������ɹ�������ʮ�Ž���Խӣ���ͼ��ʾ�����������ΪԲ���������˵������ȷ���ǣ�������| A�� | �칬һ���ڲ��Թ�����˶��ٶȴ��ڵ�һ�����ٶ� | |
| B�� | �칬һ���ڲ��Թ�����ڶԽӹ�������ڴ� | |
| C�� | �칬һ���ڲ��Թ�����ڶԽӹ���ļ��ٶȴ� | |
| D�� | �칬һ���ڲ��Թ�����ڶԽӹ���Ľ��ٶȴ� |
 ��ͼ��ʾ���ڹ⻬��Եˮƽ���ϣ���������������ĵ���M��N���ֱ�̶���A��B���㣬OΪAB���ߵ��е㣬CDΪAB�Ĵ�ֱƽ���ߣ���CO֮���F���ɾ�ֹ�ͷ�һ���������С��P������С��P��ı�ԭ���ĵ糡�ֲ��������Ժ��һ��ʱ���ڣ�P��CD�������������˶�������˵����ȷ���ǣ�������
��ͼ��ʾ���ڹ⻬��Եˮƽ���ϣ���������������ĵ���M��N���ֱ�̶���A��B���㣬OΪAB���ߵ��е㣬CDΪAB�Ĵ�ֱƽ���ߣ���CO֮���F���ɾ�ֹ�ͷ�һ���������С��P������С��P��ı�ԭ���ĵ糡�ֲ��������Ժ��һ��ʱ���ڣ�P��CD�������������˶�������˵����ȷ���ǣ�������| A�� | С��P�Ĵ�����������С�����������˶�������������ϼ�С | |
| B�� | С��P�Ĵ�����������С�����������˶�������ÿ�ξ���O��ʱ�����ʲ��ϼ�С | |
| C�� | ����M��N�ĵ���ͬʱ�����ػ���������С��p�����˶����������ڲ��ϼ�С | |
| D�� | ����M��N�Ĵ�����ͬʱ�����ػ���������С��p�����˶�������������ϼ�С |
 ��ͼ��ʾ��������Ϊ1.5kg������m1��m2�����ڶ�Ħ��������2=0.2�ĵ����ϣ�m1��m2֮��Ķ�Ħ��������1=0.3�����ú���F=12Nˮƽ������m2��ȡg=10m/s2��������
��ͼ��ʾ��������Ϊ1.5kg������m1��m2�����ڶ�Ħ��������2=0.2�ĵ����ϣ�m1��m2֮��Ķ�Ħ��������1=0.3�����ú���F=12Nˮƽ������m2��ȡg=10m/s2��������| A�� | ����m2��ֹ���� | B�� | ����m1��m2֮���Ħ������СΪ3N | ||
| C�� | ����m2�ļ��ٶ���2.5m/s2 | D�� | ����m1�ļ��ٶ���3m/s2 |
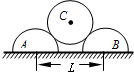 ��ͼ��ʾ����������뾶��Ϊr��������Ϊm�İ�Բ����A��B���ڴֲ�ˮƽ���ϣ�A��B����Բ�ļ�ľ���ΪL����A��B�Ϸ�һ������뾶Ϊr������Ϊ2m�Ĺ⻬Բ����C��A��B��Cʼ�ն����ھ�ֹ״̬��������
��ͼ��ʾ����������뾶��Ϊr��������Ϊm�İ�Բ����A��B���ڴֲ�ˮƽ���ϣ�A��B����Բ�ļ�ľ���ΪL����A��B�Ϸ�һ������뾶Ϊr������Ϊ2m�Ĺ⻬Բ����C��A��B��Cʼ�ն����ھ�ֹ״̬��������| A�� | B�Ե����ѹ����СΪ3mg | |
| B�� | �����A����������ACԲ�����߷��� | |
| C�� | LԽС��A��C��ĵ���ԽС | |
| D�� | LԽС�������A��B��Ħ����Խ�� |
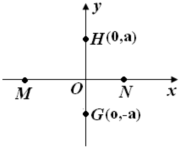 ֱ������ϵxOy�У�M��N����λ��x���ϣ�G��H����������ͼ��M��N������̶�һ�����ɣ�һ����ΪQ������������O��ʱ��G�㴦�ĵ糡ǿ��ǡ��Ϊ�㣮������������k��ʾ���������������Ƶ�G�㣬��H�㴦��ǿ�Ĵ�С�ͷ���ֱ�Ϊ��������
ֱ������ϵxOy�У�M��N����λ��x���ϣ�G��H����������ͼ��M��N������̶�һ�����ɣ�һ����ΪQ������������O��ʱ��G�㴦�ĵ糡ǿ��ǡ��Ϊ�㣮������������k��ʾ���������������Ƶ�G�㣬��H�㴦��ǿ�Ĵ�С�ͷ���ֱ�Ϊ��������| A�� | $\frac{3kQ}{4{a}^{2}}$����y������ | B�� | $\frac{3kQ}{4{a}^{2}}$����y�Ḻ�� | ||
| C�� | $\frac{5kQ}{4{a}^{2}}$����y������ | D�� | $\frac{5kQ}{4{a}^{2}}$����y�Ḻ�� |
 �߳�Ϊ15cm�������岣��ש����һ���ݣ��������ҿ�ȥ�����ݾ����6cm����������ȥ�����ݾ��Ҳ���4cm��������������Ϊ1.5�����ݾ����ʵ�����Ϊ9cm��
�߳�Ϊ15cm�������岣��ש����һ���ݣ��������ҿ�ȥ�����ݾ����6cm����������ȥ�����ݾ��Ҳ���4cm��������������Ϊ1.5�����ݾ����ʵ�����Ϊ9cm�� �õ������͵�ѹ���ⶨ�����ڸɵ�ش�����ɵĵ���飨�綯��Լ4.5V���ڵ���Լ1�����ĵ綯�ƺ��ڵ��裬���������顢����������⣬�����������Ĺ�ѡ�ã�
�õ������͵�ѹ���ⶨ�����ڸɵ�ش�����ɵĵ���飨�綯��Լ4.5V���ڵ���Լ1�����ĵ綯�ƺ��ڵ��裬���������顢����������⣬�����������Ĺ�ѡ�ã�