��Ŀ����
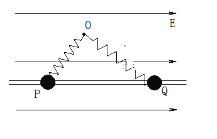
����Ŀ����ͼ��ʾ���⻬��ˮƽ���AB��뾶ΪR�Ĺ⻬�İ�Բ�ι��BCD������B�㣬ABˮƽ������ִ���ˮƽ���ҵ���ǿ�糡����Բ�ι������ֱƽ���ڣ�BΪ��͵㣬DΪ��ߵ㣮һ����Ϊm���������С��Ӿ�B��x��λ���ڵ糡�����������ɾ�ֹ��ʼ��AB�����˶���ǡ��ͨ����ߵ㣬����˵������ȷ����
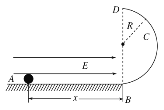
A. RԽ��xԽ��
B. m��Rͬʱ���糡����������
C. mԽ��xԽС
D. RԽ��С��B���˲��Թ����ѹ��Խ��
���𰸡�AB
��������
С��ǡ��ͨ����ߵ�ʱ���������ṩ������������ţ�ٵڶ��������С����ߵ�ʱ���ٶȣ����ݶ��ܶ���������ٶ�v0��뾶R�Ĺ�ϵ��С��B����˲�������������֧�����ĺ����ṩ����������ţ���˶������о�С��Թ����ѹ����뾶�Ĺ�ϵ��
С����BCD������Բ���˶�����D�㣬�У�mg=m![]() ��
��
��A��D���̣��ɶ��ܶ����У�qEx-2mgR=![]() mvD2����
mvD2����
�ɢ٢ڵã�![]() ����
����
��֪��RԽ��xԽ��mԽ��xԽ��A��ȷ��C������
��A��D���̣��ɶ��ܶ����У�W-2mgR=![]() mvD2����
mvD2����
�ɢ٢�ã��糡������ W=![]() mgR����֪m��Rͬʱ���糡������Խ�࣬��B��ȷ��С����B��D�Ĺ����У��ɶ��ܶ����У�-2mgR=
mgR����֪m��Rͬʱ���糡������Խ�࣬��B��ȷ��С����B��D�Ĺ����У��ɶ��ܶ����У�-2mgR=![]() mvD2-
mvD2-![]() mvB2��vB=
mvB2��vB=![]() ����
����
��B����FN-mg=m![]() ��
��
�����FN=6mg����֪С��B��˲������С���֧������R�أ���С��B���˲��Թ����ѹ��Ҳ��R�أ���D����ѡAB��